微分方程式の数値解法
目次
本日の講義では,数値的な微分方程式の解法について学びます.微分方程式は,求める道関数が一変数関数なのか,多変数関数なのかによって,常微分方程式と偏微分方程式に大別されますが,今回の講義では特に「常微分方程式」に絞って話を進めていきます.常微分方程式の数値解法においては,初期値からスタートして,微分情報を使いながら,未知関数の振る舞いを分析することが大きな目的になります.
微分方程式の数値解法
オイラー法
常微分方程式に初期条件を与えることで,関数が積分定数のような未知数を含まない形で書けるような問題を「初期値問題」と呼びます.微分方程式の数値解法は一般的にはこの初期値問題を解くことを目的にしています.
さっそく,次に示す常微分方程式の初期値問題について考えてみましょう.
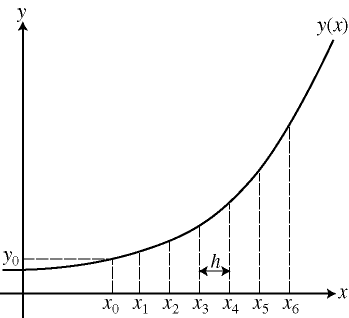
\[\frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0\]この微分方程式の解 $y = y(x)$ は,例えば,下図の曲線のようになるはずです(微分方程式の解は,一つの値ではなく関数になりますから,解は曲線で表されます).
微分方程式を数値的に解く ということは,初期値 $x_0$ から始めて,$x_1 = x_0 + h, x_2 = x_1 + h, \ldots$ における $y(x) $の値を順次求めていくことに対応します.このときの $h$ を刻み幅と呼びます.
最も単純に考えると,今 $y$ の $x$ に関する微分 $\frac{dx}{dy}$,すなわち曲線の傾きが $f(x, y)$ であるので,
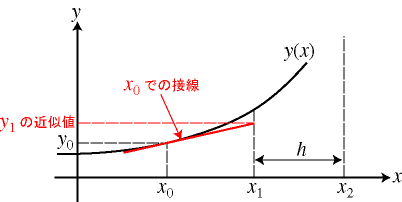
\[y(x_1) = y(x_0) + h f(x_0, y_0)\]のように近似すれば,十分に小さい刻み幅 $h$ に対しては,それなりに良い解を与えられると考えられます.これを一般化して
\[y(x_i) = y(x_{i - 1}) + h f(x_{i - 1}, y_{i - 1})\]という漸化式にしたがって,順次 $y(x_1), y(x_2), \ldots$ を求めていく方法を オイラー法 または 前進オイラー法 と呼びます.
オイラー法は,$x_0$ から $x_1$ のような幅が刻み幅に相当する区間において,傾きが $f(x_0, y_0)$ で一定であると仮定して近似解を求めることに相当します.もちろん,実際には傾きは一定では無いため,この近似が正確となりうるのは,$h \rightarrow 0$ の極限においてのみです.
陽解法と陰解法
以後の説明では,表記を簡単にするために $y_i = y(x_i)$ と書くので注意してください.
先ほど,オイラー法の公式においては
\[y_{i+1} = y_i + h f(x_{i}, y_{i})\]のように過去のデータから現在のデータを求めていました.これは $\frac{dy}{dx} = f(x, y)$ を差分法で求める際に現れる
\[\frac{dy}{dx_i}(x_i) = f(x_i, y_i) \approx \frac{y_{i+1} - y_i}{h}\]という式を変形したものとみなすことができます.このような差分の取り方を 前進差分 と呼びますが,これが上記のオイラー法を前進オイラー法と呼ぶ理由です.これと同様の考えにたつと 後退差分 の式
\[\frac{dy}{dx_i}(x_i) = f(x_i, y_i) \approx \frac{y_i - y_{i-1}}{h}\]を変形することで以下のような式を得ることができます (添字の$i$と$i-1$を1だけ増加させていることに注意).
\[y_{i+1} = y_i + h f(x_{i+1}, y_{i+1})\]この公式は 後退差分 の式から導出されるため 後退オイラー法 と呼びます.
後退オイラー法の式は,左辺と右辺の両方に$y_{i+1}$が含まれているため,今求まっている $y_i$ から単純な計算で$y_{i+1}$を求めることはできません.ですが $f(x, y)$ に具体的な関数を代入すれば,上記の方程式を代数的,あるいは数値的に解くことで,$y_{i+1}$ を求めることできます.
例えば,単純な例として$f(x, y) = x + y$ならば,上記の後退オイラー法の式は,
\[y_{i+1} = \frac{y_i + h (x_{i} + h)}{(1 - h)}\]となるため,現在の $y_i, x_i$ のみから計算が可能です.仮に $f(x, y)$ がもっと複雑であっても,数値的に方程式を解くことで$y_{i+1}$が求められる他,前進オイラー法を用いて近似した$y_{i+1}$を後退オイラー法の右辺に代入して,再度$y_{i+1}$を求める方法などもあります.
これらの前進オイラー法と後退オイラー法を比較すると,前進オイラー法は元の微分方程式に明示的に現れる (陽的な) 関数の値だけを使って解が求まるのに対して,後退オイラー法は,微分方程式を解くために追加の (陰的な) 計算が必要になってきます.
このように,次の$y_{i+1}$を求める計算が$y_{i+1}$を含まない単純な式で表される場合の解法を 陽解法 (explicit method),$y_{i+1}$を求めるために,自明でない式変形や追加の数値計算が必要になる解法のことを陰解法 (implicit method) と呼びます.
上記の例では,$y_{i+1}$を未知数とした方程式の解が,比較的簡単な形で書き表すことができましたが,より複雑なケースでは,方程式を数値的に解くことで$y_{i+1}$を求めることが一般的です.
ルンゲ・クッタ型公式
オイラー法は理論的には$h$を十分小さくすることで高い精度が得られるはずですが,現実には,
- 刻み幅 $h$ を小さくすると,計算回数が多くなる(=計算時間が増える)
- 刻み幅 $h$ を小さくすると,丸め誤差が増える
- 計算回数が多くなると,誤差の累積も増加する
という理由から,それほど良い精度は得らません.一般に微分方程式は過去のデータから次のデータを求めるために,刻み幅1つ分進むごとに生じる誤差の大きさは無視できず,実際,前進オイラー法はその精度の観点からあまり実用的とは言えません.
オイラー法は,前述の通り,関数の一階微分を差分法で近似した式から出発しています.この式は単純に刻み幅1つ分変化したときの関数の平均的な傾きと考えることもできますが,別の味方として $y(x + h)$ をテイラー展開したときに得られる
\[y(x + h) = y(x) + \frac{h}{1!} y'(x) + \frac{h^2}{2!} y''(x) + \cdots + \frac{h^n}{n!} f^{(n)}(x) + \cdots\]を1階微分の項まで用いて$h$ の一次式で近似したときに得られる式を変形したものと考えることもできます.オイラー法,特に前進オイラー法において精度が十分でない理由は,この一次式での近似に原因があります.ここでは,より精度を向上させるために,2次以上の項を用いた数値解法について見ていきます.
まず,テイラー展開を二次項まで利用した場合を考えてみましょう.多くの教科書では,まず$y(x + h)$ を近似する公式を
\[\begin{aligned} y(x + h) &= \alpha k_1 + \beta k_2 \\ k_1 &= f(x), \quad k_2 = f(x + qh, y + qh f(x, y)) \end{aligned}\]のように置いてから,未知数 $\alpha, \beta, q$を求めることが一般的ですが,ここでは二次のテイラー展開から直接公式を導いていきます.関数 $f(x, y) = \frac{dy}{dx}$を用いると,テイラー展開の式は以下のように変形できます.
\[y(x + h) \approx y(x) + \frac{h}{1!} f(x, y) + \frac{h^2}{2!} \frac{df(x, y)}{dx}\]ここで$f(x, y)$の$x$による微分を適当な刻み幅 $kh$ で計算したとすると,
\[\begin{aligned} \frac{df(x, y)}{dx} &\approx \frac{f(x + kh, y(x + kh)) - f(x, y)}{kh}\\ &\approx \frac{f(x + kh, y(x) + kh f(x, y)) - f(x, y)}{kh} \end{aligned}\]と書けるので,これを元の式に代入すると,
\[y(x + h) = y(x) + \left( 1 - \frac{1}{2k} \right) h f(x, y) + \frac{h}{2k} f(x + kh, y + khf(x, y))\]という公式が得られます.この公式において $k=1$ と置いたときに得られる
\[y(x + h) = y(x) + \frac{h}{2} f(x, y) + \frac{h}{2} f(x + h, y + h f(x, y))\]という公式を特にホイン法 (Heun’s method) あるいは改良オイラー法 (improved Euler method)などと呼びます.
また,$k=\frac{1}{2}$と置いたときに得られる
\[y(x + h) = y(x) + h f(x + \frac{h}{2}, y + \frac{h}{2} f(x, y) )\]という公式を特に 修正オイラー法 (modified Euler method) あるいは中点法 (midpoint method)などと呼びます.
このように高階の微分を単なる1階微分関数である $f(x, y)$ だけで表すような公式を ルンゲ・クッタ型の公式 あるいは単に ルンゲ・クッタ法 (Runge-Kutta method) と呼びます.上記のホイン法と改良オイラー法はいずれも2次のルンゲ・クッタ法です.
課題1 (配点: 2点)
以下のスケルトンプログラムを元にして, $f(x, y) = x + y$, $x_0 = y_0 = 0$ の場合の誤差を 前進オイラー法, 後退オイラー法, ホイン法, 修正オイラー法 の間で比較せよ.なお,上記の微分方程式の解は, $y = -(1 + x) + e^x$ である.
なお,この例では,微分方程式が「硬い方程式」と呼ばれるような急激に値が変化する形をしていないので,後退オイラー法のような陰解法の利点を知ることが難しい.興味がある人は$y’(x) = -16y$, $y(0) = 1$として微分方程式を解いてみると良い.この微分方程式の解は$y = e^{-16x}$であるが,このときに刻み幅を$h=0.25$程度にすると陽解法では解が発散してしまう.
#include <stdio.h>
#include <math.h>
double f(double x, double y) {
return x + y;
}
double answer(double x) {
return -(1.0 + x) + exp(x);
}
double eulerf(double x, double y, double h, double (*f)(double, double)) {
// 前進オイラー法
}
double eulerb(double x, double y, double h, double (*f)(double, double)) {
// 後退オイラー法
}
double heun(double x, double y, double h, double (*f)(double, double)) {
// ホイン法
}
double euler2(double x, double y, double h, double (*f)(double, double)) {
// 修正オイラー法
}
int main() {
const int N = 100;
const double h = 5.0 / N;
const double x_0 = 0.0;
const double y_0 = 0.0;
double y_true;
double x = x_0;
double y = y_0;
double error = 0.0;
for (int i = 0; i < N; i++) {
y = euler2(x, y, h, f);
x = x + h;
y_true = answer(x);
error += (y_true - y) * (y_true - y);
printf("%f %f %f\n", x, y, y_true);
}
error = sqrt(error / N);
printf("Error: %.8f\n", error);
}
高階ルンゲ・クッタ法
単に「ルンゲ・クッタ法」といった場合,一般的には,4次のルンゲ・クッタ法を指します. 4次のルンゲ・クッタ法は,テイラー展開の4次項までを残したときに,上記と同様の計算を繰り返し行うことで得られる公式で,一般には
\[\begin{aligned} y(x + h) &= y(x) + h (\alpha k_1 + \beta k_2 + \gamma k_3 + \delta k_4) \\ k_1 &= f(x, y) \\ k_2 &= f(x, y + qh k_1) \\ k_3 &= f(x, y + rh k_2 + sh k_1) \\ k_4 &= f(x, y + th k_3 + uh k_2 + vh k_3) \end{aligned}\]のように書けます.この中で代表的なものが,
\[\begin{aligned} y(x + h) &= y(x) + \frac{h}{6} (k_1 + 2 k_2 + 2 k_3 + k_4) \\ k_1 &= f(x, y) \\ k_2 &= f(x + \frac{h}{2}, y + h \frac{k_1}{2}) \\ k_3 &= f(x + \frac{h}{2}, y + h \frac{k_2}{2}) \\ k_4 &= f(x + h, y + h k_3) \end{aligned}\]とするもので,一般にルンゲ・クッタ法というときにはこの公式を指します.
課題2 (配点: 2点)
課題1で用いたプログラムに4次ルンゲ・クッタ法の関数を付け足して,その他の方法と誤差を比較せよ.
より一般的な常微分方程式
連立微分方程式
次のような連立微分方程式を考えてみましょう.
\[\begin{aligned} \frac{dy_1}{dx} = f_1(x, y_1, y_2, y_3) \\ \frac{dy_2}{dx} = f_2(x, y_1, y_2, y_3) \\ \frac{dy_3}{dx} = f_3(x, y_1, y_2, y_3) \end{aligned}\]これは $\mathbf{y}$ および $\mathbf{f}$ を
\[\mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix}, \quad \mathbf{f}(x, \mathbf{y}) = \begin{pmatrix} f_1(x, y_1, y_2, y_3) \\ f_2(x, y_1, y_2, y_3) \\ f_3(x, y_1, y_2, y_3) \\ \end{pmatrix}\]として定義することで,
\[\frac{d \mathbf{y}}{dx} = \mathbf{f}(x, \mathbf{y})\]という形で書き表すことができます.これは,前節までで扱った微分方程式と同じ形であるので,同様の方法で解くことが可能です.例えば,ルンゲ・クッタ法の場合なら,
\[\begin{aligned} \mathbf{y}_{i+1} &= \mathbf{y}_i + \frac{h}{6} (\mathbf{k}_1 + 2 \mathbf{k}_2 + 2 \mathbf{k}_3 + \mathbf{k}_4) \\ \mathbf{k}_1 &= f(x, \mathbf{y}) \\ \mathbf{k}_2 &= f(x + \frac{h}{2}, \mathbf{y} + h \frac{\mathbf{k}_1}{2}) \\ \mathbf{k}_3 &= f(x + \frac{h}{2}, \mathbf{y} + h \frac{\mathbf{k}_2}{2}) \\ \mathbf{k}_4 &= f(x + h, \mathbf{y} + h \mathbf{k}_3) \end{aligned}\]のようにして解くことが可能です.これは $y$, $f$, および $k$ がベクトル表記になっている以外は前節の形式と全く同じです.
高階微分方程式
高階微分方程式(上記で「高階」ルンゲ・クッタと言った時の「高階」とは別)は,変数の微分を新しい変数として付け加えることで,連立の1階微分方程式に置き換えることができます.
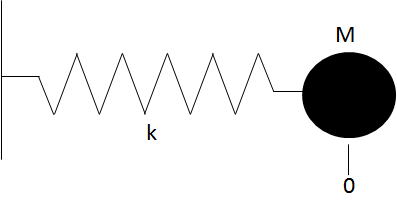
例えば,質点-バネモデルの運動方程式を考えてみましょう.以下,上記と異なるので紛らわしいですが,位置を$y$が時間$t$の関数であるとして,その二階微分を含む微分方程式が,バネ定数 $k$ と 質点の質量 $m$ を用いて,
\[\frac{d^2 y}{dt^2} = -\frac{k}{m} y\]と表されるとします.これは,新しい変数として$y$の微分$y’$を考えて,
\[\begin{aligned} y_1' &= y_2 \\ y_2' &= -(k / m) y_1 \end{aligned}\]という連立微分方程式に書き直すことができます.よって,これは前節で述べた手法で解くことができます.
固有振動解析プログラムの作成
今回の授業では,実用的なバネ振動系の固有振動数解析ソフトを作成してもらいます.
- ルンゲ・クッタ法による連立微分方程式解法のサブルーチンのプログラミングをします.
- 下記に示すバネ振動系において,ルンゲ・クッタ法を用いて,おもりの時間に対する振動軌跡を計算します.
- 計算した振動軌跡をファイルへ出力し,MATLABでスペクトル解析して固有振動数を求めます.
- 数値計算により算出した固有振動数と理論解が一致しているとを確認し,プログラムが正しいことを証明します.
高校の物理風に書くと $ m a = - ky$,大学の物理風に書くと$y’’ = -(k / m) y$という常微分方程式になります.
ばね定数 $k$ [N/m]のばねの片端を固定し,片端に質量 $m$ [kg] を付けた時の固有振動数 $f_0$ [Hz] は
\[f_0 = \frac{1}{2 \pi} \sqrt{\frac{k}{M}}\]と簡単に計算できます.
したがって,おもりの時間に対する軌跡をルンゲ・クッタ法による数値計算により求め,その結果をフーリエ変換すれば,最大振幅の周波数は,上記と理論式と一致するはずです.
それを証明してもらいます.
課題3 (配点: 2点)
本節で説明したルンゲ・クッタ法による連立微分方程式の解法をプログラミングしたい.
任意の$x$と,その$x$における$\mathbf{y}(x) = \mathbf{y}_0$の値と刻み幅$h$ならびに$\frac{d\mathbf{y}}{dx}$を与えると,4次ルンゲ・クッタ法により刻み幅$h$だけ進んだ$x + h$における$\mathbf{y}(x + h) = \mathbf{y}_1$ の値を返す関数を作成する.
計算の方法については,これまでに解いた演習課題と同様であるが,高階の微分方程式においては,ルンゲ・クッタ法で扱う変数が2つになるため,関数のプロトタイプ宣言は matrix 型を用いて以下のような形となる.
void runge_kutta(double x, matrix y0, double h, matrix *y1, void (*f)(double, matrix, matrix *));
第5引数として与える関数は void f(double x, matrix y, matrix *dydx)のような関数であるとする.この関数はこれまでのfの定義と異なり$\frac{dy}{dx}$の値を戻り値として与える代わりに,引数として与えられる matrix の値を書き換えるものとなっているので注意すること.
このようにして作成したルンゲ・クッタ法の関数を繰り返し呼び出して,単振動の軌道を計算せよ.なお,関数を繰り返し呼び出す回数は1024回とすること.
また,質点の質量 $m$ ならびにバネ定数 $k$ は scanf 関数を用いて,プログラム実行中に変更できるようにすること.
データを取り出すに当たっては
FILE *fp = fopen(argv[1], "w");
...
fprintf(fp, "%f, %f, %f\n", t, mat_elem(y0, 0, 0), mat_elem(y0, 1, 0));
...
fclose(fp);
のようにして計算結果をCSV形式でファイルに出力するようにし,プログラム実行時には
./a.out output.csv
とすることで,Excel等を用いてグラフを作成することができるようにすると便利である (main関数の引数で宣言が必要).使い方がわからない場合はソースコード内にファイル名を直接打ち込んでも良い.
注意
- この課題では
matrixライブラリを利用します. - この課題用に,新しいディレクトリを一つ作成してください.
- ソースコードのコンパイルは自身でMakefileを作る(前回の
least_squareの課題で用いたものが参考になる)のが好ましいですが,難しければ単純にmatrix.cならびにmatrix.cを上記のディレクトリにコピーしてGCCを使用してコンパイルしても構いません. -
runge_kutta関数の引数である $y_0$ と $y_1$ に同じ変数を指定しても正しく動作するようにしてください(普通にプログラムする限りは,気にせずとも大丈夫だと思います)
課題4 (配点: 2点)
課題3で得た単振動の軌跡のデータを入力とし,MATLABを用いてパワースペクトルのピーク位置を調べよ.MATLABを用いたスペクトル解析の方法については,MATLABを用いた数値解析の入門 で学んだことを参考にすると良い.また,MATLABを用いてCSVファイルを読み込むには readmatrix 関数 (ドキュメント) が使える.
なお,パワースペクトルは以下の注意に示すような手順で計算できるが,今回の課題ではピークの位置が正しく出ていれば良いものとする.
注意
パワースペクトルは積分区間を$[0, T]$としたときに,次のように計算できる.まず,時間方向に正規化されたフーリエ変換を以下の式で求める.
\[\mathcal{F}[f](\omega) = \frac{1}{\sqrt{T}} \int_0^T f(t) \exp(-i \omega t) dt\]MATLABのfft関数は上記の式における$dt$の大きさを考慮しないことに注意し,サンプリング数を$n$として$T / n$だけスケールされる必要があることに注意する.(実際fft関数は$dt$の大きさを引数に取らない).パワースペクトルはこのフーリエ変換された信号の強度の二乗として,以下のように定義される.
パワースペクトルの大きさはパーセバルの定理を満たすように正規化される必要があり,パワースペクトルの積分は元々の信号の強度の時間平均に等しくなる.MATLABのfft関数を用いて得られるフーリエ変換結果の定義域は1周期分で$[0, 1]$だと考えて良いので,以下の等式が成り立つ.
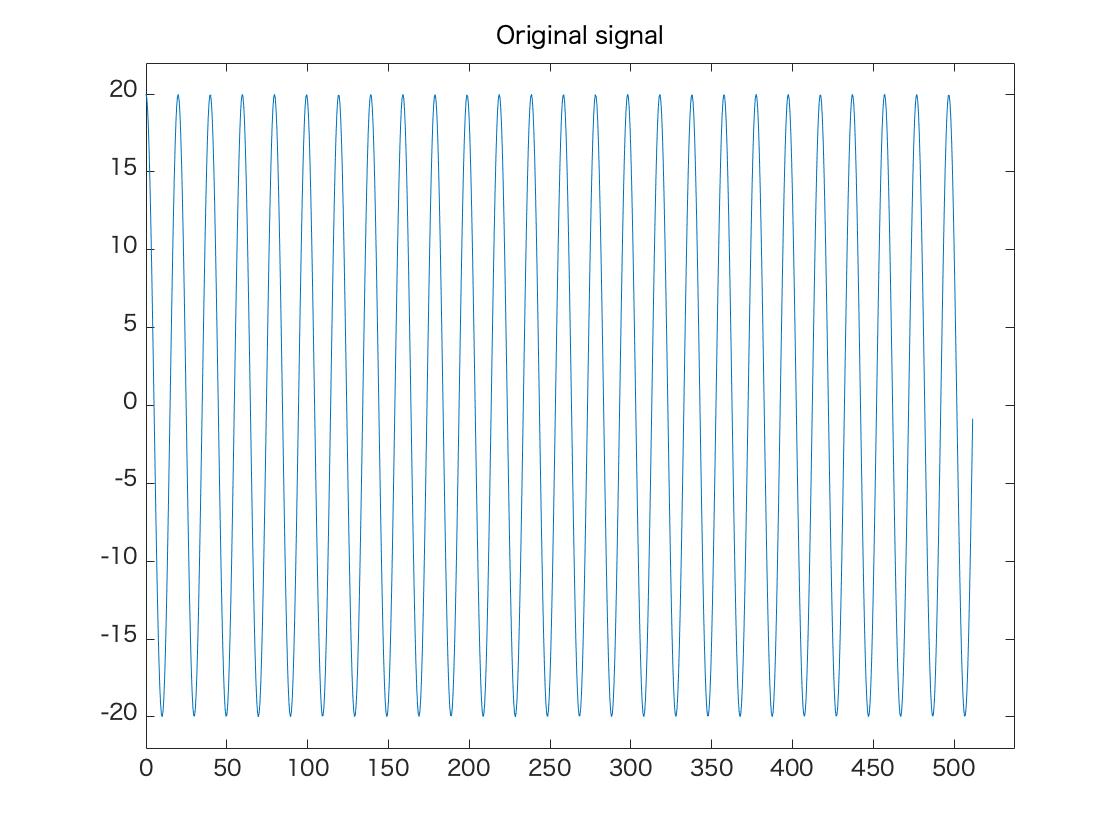
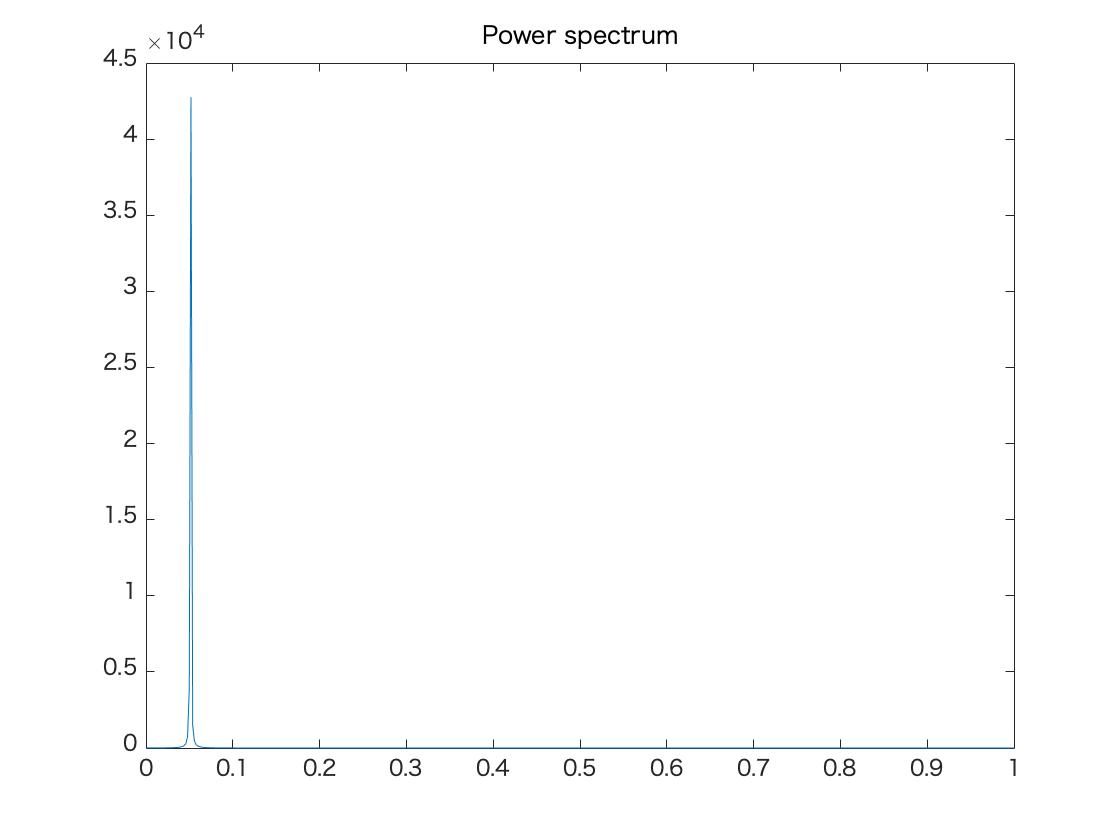
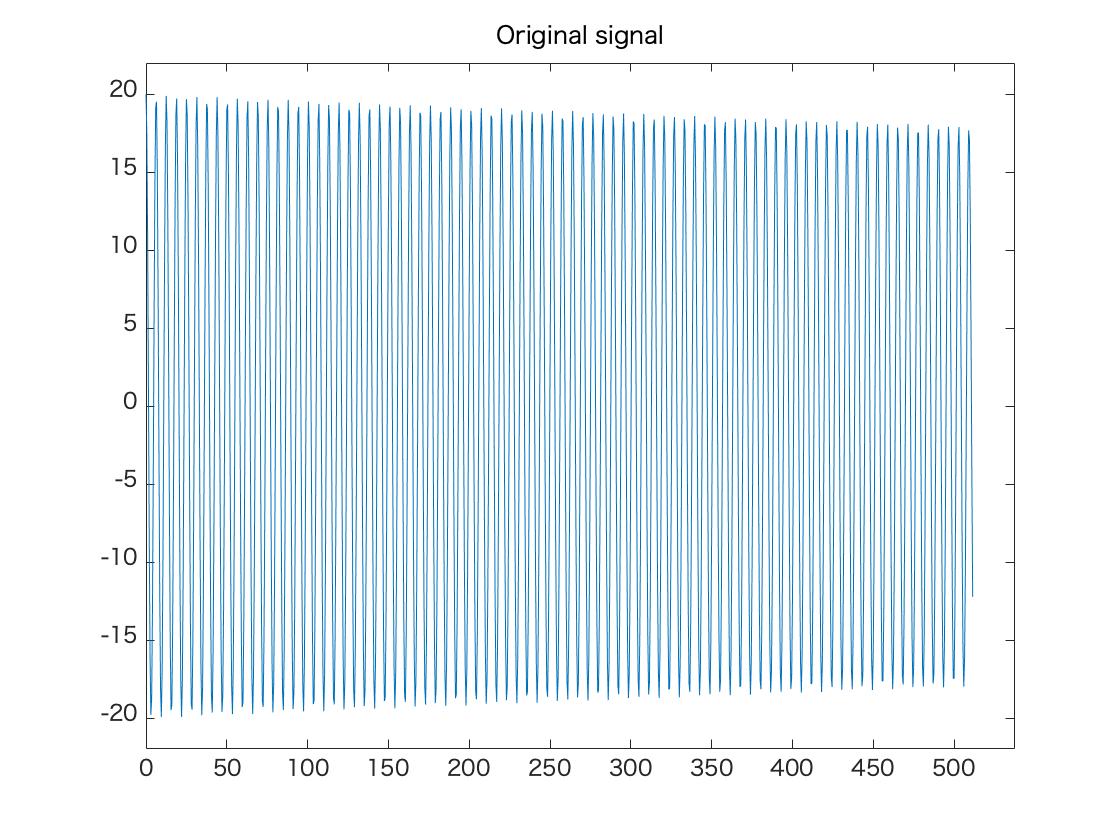
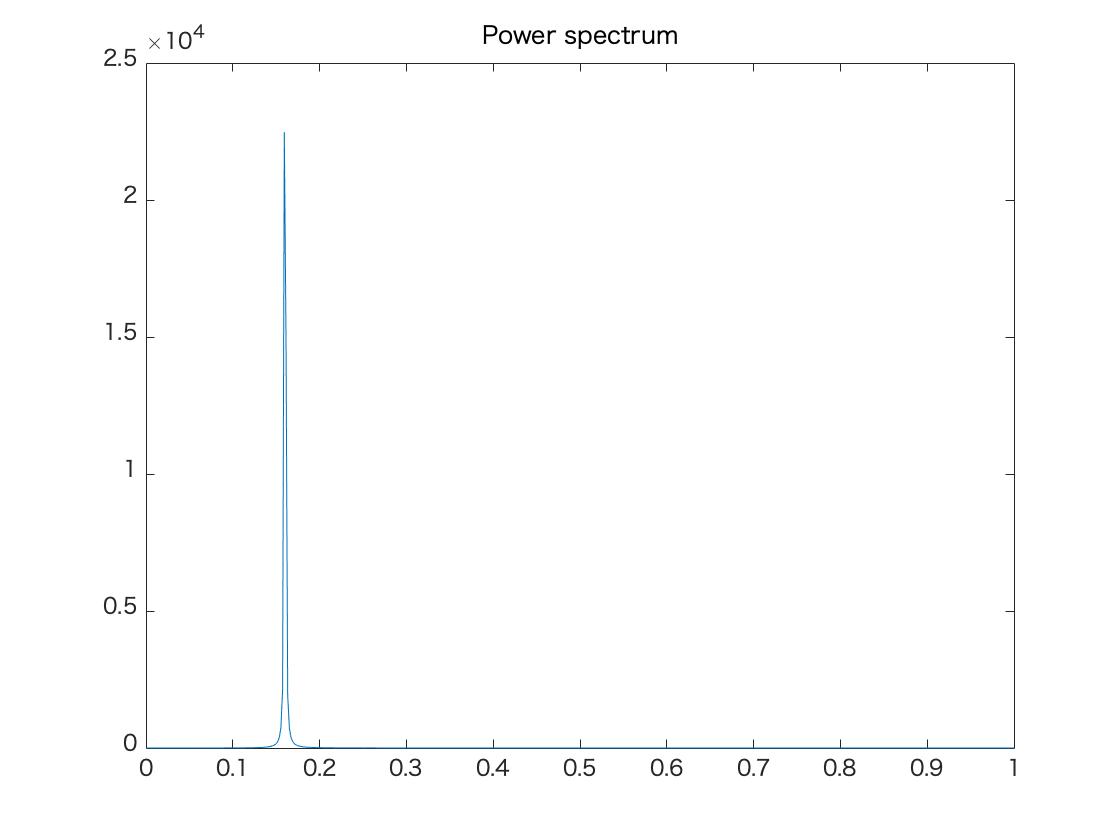
以下の例では刻み幅が$h = 0.5$でこれを1024ステップ動かすので$T = 512$となる.正しく解析ができると,単振動,パワースペクトルのグラフ,ならびに固有振動数は以下のようになる.
条件1
| 質量 $m$ | 100 kg |
| ばね定数 $k$ | 10 [N/m] |
| 変位の初期値 $y_0$ | 20 [m] |
| 刻み幅 $h$ | 0.5 [s] |
シミュレーションによる固有振動数
0.050781 [Hz]
理論値の固有振動数
0.050329 [Hz]
|
|
条件2
| 質量 $m$ | 10 kg |
| ばね定数 $k$ | 10 [N/m] |
| 変位の初期値 $y_0$ | 20 [m] |
| 刻み幅 $h$ | 0.5 [s] |
シミュレーションによる固有振動数
0.15820 [Hz]
理論値の固有振動数
0.15915 [Hz]
|
|
課題5 (配点: 2点)
課題3で扱った微分方程式に重力の影響と速度に対する抗力の項を追加し,減衰振動となるようにした方程式
\[m \frac{d^2 y}{dt^2} = -ky + mg - c \frac{dy}{dt}\]を考える (上記の方程式では鉛直下向きを正としている).
重力加速度を $g = 9.8$ [N],抗力係数を $c=1.0$ [kg/s] として,課題3, 4と同様の解析を行なって,
- 固有振動数は抗力や重力の影響で変化しないこと
- 質点の変位がばねと重力の釣り合いの位置に収束すること
を確かめよ.