MATLABによる数値解析入門

目次

• MATLABの基本
  • MATLABのインストール
  • 基本的な使い方 (MATLABドキュメント)
  • 方程式の解法
  • 課題1 (配点: 2点)
  • 課題2 (配点: 2点)
• フーリエ解析
  • 離散フーリエ変換 (簡易版)
  • 練習問題1
  • 練習問題2
  • 高速フーリエ変換
  • 高速フーリエ変換の応用
  • 課題3 (配点: 2点)
• 常微分方程式の求解
  • 常微分方程式の数値解法
  • 練習問題3
  • 高階微分方程式の解法
  • 課題4 (配点: 2点)
  • 課題5 (配点: 2点)

MATLABの基本

MATLABのインストール

MATLABのインストール方法についてはMATLABのインストールを見てください．

基本的な使い方 (MATLABドキュメント)

MATLABの公式のドキュメントにアクセスし，MATLABの基本的な使い方についての解説を読んでください．

• MATLAB - 例

ページにアクセスすると，左側のメニューに「MATLAB」というリンクがあるので，ここをクリックし，現れるカテゴリの中から以下のチュートリアルを読んでください．

• MATLAB入門
  • 行列および配列
  • 配列インデックス付け
  • 関数の呼び出し
• 言語の基礎
  • 行列の作成，連結，および拡張
  • 配列インデックス付け
• グラフィックス
  • 二次元ラインプロットの作成
  • チャートへのタイトルと軸のラベルの追加
  • 複数プロットの結合
  • 軸の範囲の指定

方程式の解法

計算機を用いて方程式の解を求める場合，通常は数値解法と呼ばれるコンピュータ上での計算に特化したアルゴリズムが使われるのが一般的です．例えば， $\sqrt{2}$ の値を求めたいときに， $x^2 = 2$ の解を数値的に求めたいとすれば，二分法やニュートン・ラフソン法などが用いられる，といった具合です．

その一方で，計算機上で人間が方程式を解く過程を模した仕組みに記号計算と呼ばれるものがあります．例えば，上記の $x^2 = 2$の解を求める場合，数値解法では $x = 1.41421356…$ のような数値が得られるのに対して，記号計算においては $x = \sqrt{2}$ という数学上の記法を使った解を出力することができます．

MATLABにはこのシンボル計算を行うためのライブラリが用意されていて，以下のように入力することで，その違いを見ることができます．

% 記号変数xを定義
syms x;

% 記号関数fを定義
f(x) = x.^2.0;

% 記号計算により求解 (最後のセミコロンがないことに注意)
solve(f(x) == 2.0, x)

正しく計算が行われると，

ans =
  2^(1/2)
  -2^(1/2)

のようにべき乗の形で解が得られるはずです．

記号計算を使った方程式の求解については，MATLABのドキュメンテーションにある以下の項目を読んでください．

• 代数方程式の求解

上記の記号計算は，直感的であり，とても便利に思えますが，必ずしもそれが使える事ばかりとは限りません．とある方程式の解が，四則演算やべき乗，対数，三角関数などの組み合わせで書けるとき，その方程式が「解析的に解ける」といいます．記号計算は，まさに解析的に解けるケースに対しては，その解析解，すなわち四則演算やべき乗を組み合わせた解を返してくれます．しかしながら，解析的に解けないケースについてはその限りではありません．

例えば，

$ \log(\log x) = \frac{1}{2} x - 4 $

という方程式の解を記号計算を使って求めてみます．

syms x;
f(x) = log(log(x)) - 0.5 .* x + 4.0;
solve(f(x) == 0.0, x)

すると，

警告: シンボリックに解くことができません．vpasolve を使用して数値解を返しています． 
> In solve (line XXX) 
 
ans =
 
9.6355556294127643341334828234735

のような結果が得られるはずです．これは上記の方程式が解析的な解を持たず，記号計算では解けないことを意味しています．その代わりに，方程式を数値的に解く関数である vpasolve を用いて解を求めています． vpasolve の使い方についてはMATLABのドキュメントを見て確認してください．

• 方程式の数値的な求解

ここまでを踏まえて，以下の3つの課題をやってみましょう．

課題1 (配点: 2点)

以下の2つの代数方程式について，右辺と左辺をグラフとしてプロットし，実数解を全て求めよ．ただし(2)については記号計算では解が求まらない．その理由を考察し，数値的に全ての解を求めよ．

課題2 (配点: 2点)

「方程式の解法」で学んだことを元にして，以下の行列の固有値を 特性方程式 を解くことによって求めよ． また，MATLABの eig 関数を用いて，同じ行列の固有値を求め，特性方程式から求めたものと比較せよ．

フーリエ解析

ここでは，フーリエ解析の数学的な背景や導出については触れませんが，MATLABを用いたフーリエ解析の方法について，プログラムを通して学びます．

フーリエ変換は，とある関数 (ここでは実数値とする) を周波数の異なる正弦波と余弦波の足し合わせにより表現し直す変換です．ここではまず，MATLABの使用例にある以下のドキュメントを読み，単純な解析の方法について理解してください．

• フーリエ変換とフィルター処理
  • FFTを利用した周期データの解析
  • スペクトル解析のためのFFT

離散フーリエ変換 (簡易版)

フーリエ変換は，一般に

のように書き表せます．これを離散化することで得られるのが離散フーリエ変換です．この積分を離散化するために，まずフーリエ変換される関数 $f(t)$ をデルタ関数を使って

のように表します．これは，$t$ が整数のときにだけ関数が値を取るように離散化したものです．これをフーリエ変換の式に代入すると，

となります．この被積分関数だけが離散化された形のフーリエ変換を特に 離散時間フーリエ変換 (discrete-time Fourier transform) と呼びます．しかしながら，この形は信号が無限に大きな定義域上で定義されているため，有限の領域で定義されていることが多い離散信号 (あるいはデジタル信号) を扱いづらいという側面があります．そこで，離散信号が局在化していると考え，$f(n)$ が $n=0, 1, \ldots, N-1$ でのみ非ゼロであるとすると，DTFTの式をさらに以下のように書き直せます．

離散フーリエ変換では慣習的に，この $n=0, 1, \ldots, N-1$ という離散量が $[0, 2\pi]$ という定義域に対応していると考えます．今，$n$ を間隔$1$ でサンプリングしていることから，領域の大きさが $2 \pi$であるなら，単位周波数は $\frac{2 \pi}{N}$ となり $\omega_k = \frac{2\pi k}{N}$ と離散化できます．これを上の式に代入し $F(\omega_k) = F(k)$ と書くことで，

という離散フーリエ変換の式が得られます．また，ここでは導出を省略しますが，逆フーリエ変換は

のようにかけます．なお係数に現れる $\frac{1}{N}$ は文献ごとにフーリエ変換側につくのか，逆フーリエ変換側につくのかが変わっていますが，計算上は大きな問題はないので，それぞれの文献に合わせた表記で理解することをおすすめします．

なお，上記の導出では，教科書にある離散フーリエ変換の定義を導出しましたが，MATLABにおいては周波数領域を特に正規化していないため，フーリエ変換により得られる信号の定義域は $n = 0, 1, \ldots, N-1$ のままになっています．

練習問題1

MATLABのドキュメントにある フーリエ変換 のページを参考に，

のフーリエ変換を周波数領域の中心が原点になるようにプロットし，現れるピークの位置について考察せよ (ピークの数と位置)．

練習問題2

上記の練習問題において，関数の定義域を $N$ 分割して得られる離散信号をフーリエ変換するのにかかる時間を時間計測関数 tic ならびに toc によって計測し $N$ が2倍, 3倍, 4倍となった時に計算時間がそれぞれ何倍になるかを調べよ．

高速フーリエ変換

上記の離散フーリエ変換の計算を使って $F_k$ を $k = 0, 1, \ldots, N-1$ の全てに対して求めるための計算量はどのくらいでしょうか？一つ一つの係数を求めるためには $n=0, 1, \ldots, N-1$ 個の数値を求めて足しあげる必要がありますので，計算量は $O(N)$ (要素数 $N$ に比例する計算量，ということ) と見積もられます．したがって，全体では離散フーリエ変換にかかる計算量は $O(N^2)$ と考えられます (前述の練習問題ではどうだったでしょうか？)

一方で，離散フーリエ変換の式をうまく変換してやると，もっと少ない計算量で同じ計算を実現することができます．

指数の係数を $w_N = \exp(2 \pi i)$ のように表し，離散フーリエ変換の式を行列形式で書き直すと，次のような関係式が得られます．

以後，動作を直感的に理解するために $N=4$ であると仮定する．すると，上の式は以下のように書き直せます．

さらに，右辺に現れる $f_n$ の順序を添字の偶奇を元に入れ替え，それに応じて行列の列順序も入れ替えます．ここで， $w_N^N = w_4^4 = 1$ であることに注意すると，

この行列の $2 \times 2$の4つのブロック成分に注目すると，最初の2列現れるブロッグ行列は同じであり，後半の2列に現れるブロック行列は，各行がそれぞれ，$w_N^r$ ($r$ は行番号 倍になっていることがわかる．したがって，この係数行列は以下のように分解できます．

この係数行列の構成に注目すると，一つ目の係数行列は左2列が単位ブロック行列からなっていて，右2列が各行をスケーリングする行列となっています．したがって，この行列をかけるときに必要な計算は掛け算が $N$ 回 (1を掛け算する必要はないため) と足し算が $N$ 回です．したがって，この行列をかける計算量は掛け算がより計算量に対して支配的であると考えて $O(N)$ と見積もられます．

さらに二つ目の行列に注目すると，ブロック体各成分は長さが $2$ の離散信号に対する離散フーリエ変換に現れる係数と同じになっていることが分かります．この結果から，帰納的に考えると， $N$が$2のべき乗であるような場合には，離散フーリエ変換の計算が $N$ 回の掛け算と $N$$ 回の足し算を伴う計算と，2分の1のサイズの離散信号に対する離散フーリエ変換2回に分解されると予想され，実際にそのようになります．

この操作を一度行うと，必要な離散フーリエ変換をするべき信号の長さ2分の1ずつになっていき，その長さは最終的に1になるまで減らせることから，この分解は $N=2^m$ であれば $m$回，すなわち $ \log_2 N $ 回だけ行えば十分です．1回の操作にかかる計算量は上記の通り $O(N)$ であるので， $\log_2 N$ が底の変換により $\log N$ のスカラー倍であることに注意すれば，この計算全体にかかる計算量は $O(N \log N)$ まで減少することが分かります．

高速フーリエ変換の応用

高速フーリエ変換の応用は様々ありますが，ここではフィルタ処理の高速化について紹介します．

フーリエ変換には関数の畳み込み積分を関数同士の積に分解するという性質が知られています．関数 $f$ と $g$ の畳み込み積分は以下の式で与えられます．

この畳み込みの結果のフーリエ変換 $\mathcal{F}(f \ast g)$ は，各関数のフーリエ変換 $F, G$ を用いて以下のように表されます．

単純に考えれば $f$ と $g$ の定義域が同じで，その定義域から $N$ 点がサンプリングされているとすれば，離散的な畳み込み積分により，この $N$ 点全てにおける $(f \ast g)$ を計算するために $O(N^2)$ の計算時間が必要となります．

一方で，高速フーリエ変換の計算量は $O(N \log N)$ であったので，一度，二つの関数をフーリエ変換 (計算量 $O(N \log N)$) してしまい，$N$ 点における $F$ と $G$ の値を掛け算 (計算量 $O(N)$) して，それをさらに逆フーリエ変換 (計算量 $O(N \log N)$)すると，より少ない計算量で同様の結果が得られることが分かります．

なお，上記の畳み込みの計算は離散的には巡回行列とベクトルの積に対応している．被畳み込み関数 $f$ が離散的に

と表されるとすると，この畳み込みは (定義域のシフトを正しく調整すれば)

と信号のベクトル $[ g_0, g_1, \cdots, g_{N-1} ]$ との積で書けます．この巡回行列との積の計算も，単純に計算すれば $O(N^2)$ の計算コストであるが，FFTを利用することで効率的に計算できることは，特に信号処理などの分野において大変重要です．

実際に以下の課題に取り組んで，計算量が実際に少なくなっていることを確認してください．

課題3 (配点: 2点)

(1) 一次元信号 $\sin x + \cos 2 x$ と $\exp(-x^2 / 4)$ の畳み込み積分を $x \in [-\pi, \pi]$ の範囲で計算し，グラフとしてプロットせよ．計算には conv 関数を使って良いが，離散信号の長さが変化するので，第3引数に 'same' を与えること．

(2) (1)で得られた畳み込み結果とFFTを用いた計算で得られる畳み込み結果が一致することをグラフとしてプロットすることで確認せよ．

(2) に取り組むにあたって，FFTを用いた計算法は畳み込む関数 $f$ が定義域の外側でも周期的に繰り返していると仮定するために，(1)と若干結果は異なる．なお，巡回行列の積として畳み込み積分を表した場合には，FFTの場合と同様の信号が得られる．また，逆フーリエ変換時に定義域がシフトするので，それを ifftshift で修正すること．

また，上記のconvを用いた計算は離散的な信号のサンプリング間隔が1だと思って計算をするため，畳み込みにより得られる関数の縦軸の値がおかしくなる可能性がある．正しく，畳み込みの値を計算するには，信号のサンプリング間隔を畳み込みの結果に掛け算する必要があります．

例えば $[-\pi, \pi]$ の範囲を1000個に分割するとすると

N = 1000;
xs = linspace(-pi, pi, N);
dx = 2.0 * pi / N;
fs = ???;  % 適宜評価する
gs = ???;  % 適宜評価する
hs = conv(fs, gs, 'same') .* dx;

のようにすれば正しい畳み込みの結果が得られます．

常微分方程式の求解

ここでは，次回以降に行うC言語での微分方程式の数値解法に先立って，MATLABで常微分方程式の解法に触れてみます．以下の微分方程式について考えてみましょう．

微分方程式の数学としての解き方は別の教科書等に任せることにして，この一般解をMATLABをつかって求めます．本日の冒頭で学んだ代数方程式の解法と同様，微分方程式の解も記号計算による解法と数値解法の両方が用意されています．まずはシンボル計算で微分方程式を解いてみます．

MATLABのドキュメントにある常微分方程式の求解を参考にすると，以下のようにして嬢微分方程式を解くことができます．

syms x y(x);
eqn = diff(y, x) == y + x;
S = dsolve(eqn);

なお，このプログラム中に現れる diff は第一引数に与えられたシンボル関数を第二引数に与えられた変数で微分する記号計算用の関数です．実際に，disp(S) で解を表示してみると C3*exp(x) - x - 1 のように表示され，先の微分方程式の解が

であることが分かります．実際，この$y(x)$を微分してみると，元の微分方程式が確かに満たされていることが分かります．

続いては，この微分方程式に境界条件を与えてみます．先ほど用いた dsolve は第2引数に境界条件を取ることもできます．

cond = y(0) == 0;
S = dsolve(eqn, cond);

すると，今度は解がexp(x) - x - 1となり，確かに境界条件が反映されていることが分かります．

常微分方程式の数値解法

上記の例では，微分方程式の解が「数式」の形で得られており，記号計算で処理が完結していることが分かります．ところが，このような記号計算による求解が可能となるのは常微分方程式が，閉形式の解，すなわち積分を除く四則演算や三角関数，指数対数などの初等関数の組み合わせによる式で与えられる場合だけです．

例えば，多項式の分数で表されるような関数をその導関数に持つような関数は閉形式で書くことができますが，その分母と分子が多項式ではない場合，例えば，

のような微分方程式は，閉形式の解を持ちません．実際，MATLABを用いてこれを数値的に解こうとしてみましょう．

syms y(x);
eqn = diff(y) == (x - exp(-x)) / (y(x) + exp(y(x)));
dsolve(eqn);

すると，MATLABが記号計算により閉形式の解を与えることが出来なかった旨を表すエラーメッセージが表示されます．

そこで，式としての微分方程式の解を得ることはあきらめて，解を数値的に求めることを試みます．MATLABにはいくつかの数値解法ソルバーが用意されていますが，今回はルンゲ・クッタ型の常微分方程式解法の一種で，5次の解法であるドルマン＝プリンス法を用いたode45 という関数を使います．

MATLABドキュメントのode45の使い方によれば，以下のようにして数値解を得ることができます．

tspan = [0 5];    % xが [0, 5] の区間内で数値解を求める
y0 = 0.0;         % yの初期値 (x = 0) は0
[x, y] = ode45(@(x, y) (x - exp(-x)) / (y + exp(y)), tspan, y0);

すると今度はエラーが出ずに計算が終了し，

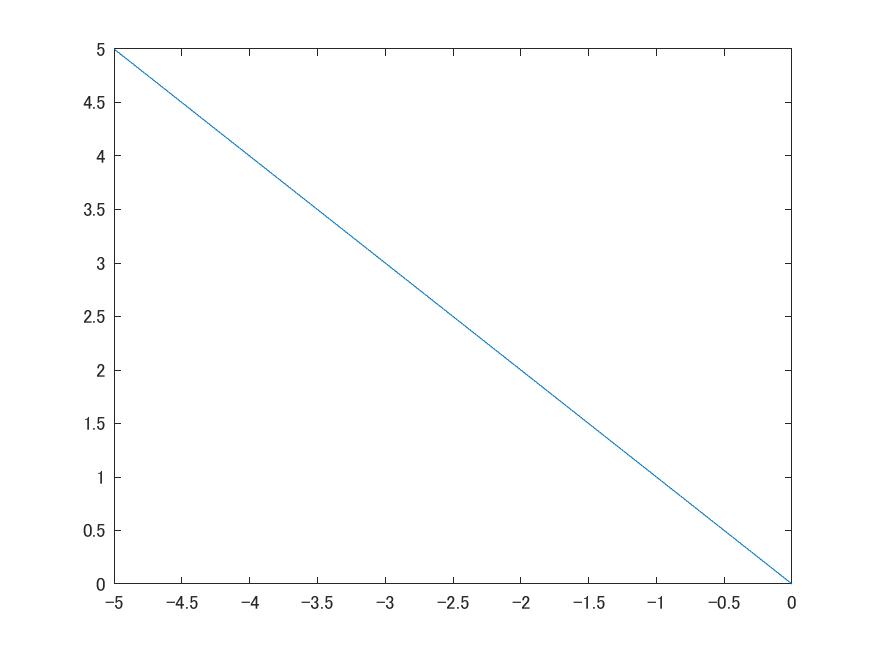
plot(x, y);

として，計算結果をプロットすると以下のようなグラフが得られます．

なおプログラム中に @(x, y) ... という書き方が登場しますが，これは x と y を引数に取り ... を返す関数，という意味です．ここには記号計算で定義した関数は入れることができないため，y(x)ではなくyが使われていることに注意してください．

練習問題3

上記の微分方程式

の数値解と記号計算で求めた関数をグラフとしてプロットし，その軌跡を比較せよ．

高階微分方程式の解法

次に2階微分が入った微分方程式

を数値的に解いてみます．実は ode45 の第一引数には一階導関数しか取ることができません．そのため，上記の式をそのまま ode45 で解くことはできません．

そこで，上記の式を次のように変形します．

この連立常微分方程式に含まれるそれぞれの方程式は線形の方程式になっているので，これは要素を配列のように持つことで解くことができます．

dfun = @(x, y) [y(2); -5.0 * y(1)];
xspan = [0 5];
y0 = 1;
z0 = 1;
[x, y] = ode45(dfun, xspan, [y0; z0]);

課題4 (配点: 2点)

上記の2階常微分方程式

は， $y$が変位を $x$ が時間を表すと考えると，バネに繋がれた重りに対する運動方程式だと考えられる．この方程式に対して速度に応じて抗力を与える空気抵抗の項を追加し，微分方程式の解が減衰振動となるようにせよ．この際，空気抵抗の項に与える係数は各自適当に指定しよいが，この係数が減衰に関与することを念頭において，振動の減衰が確認できるように調整すること．

その微分方程式を記号計算と数値計算の両方で解き，両方の結果をグラフとしてプロットせよ．

課題5 (配点: 2点)

ロトカ・ヴォルテラの方程式として知られる以下の連立常微分方程式

を $c_1 = 6.0$, $c_2 = c_3 = 1.0$, $c_4 = 4.0, x(0) = 3, y(0) = 2$ の元で解き，結果をグラフとしてプロットせよ．この際，記号計算による解法と数値解法の両方を試みて，記号的に解けるかどうかも確認すること(一般的には解けない)．結果として得られる関数$x(t)$, $y(t)$の振る舞いは$c_1, c_2, c_3, c_4$の値や，$x$, $y$に与える初期値によって，グラフの形が大きく変化するので，自分でいろいろ試してみると良い (特に$c_1 \neq c_4$かつ$c_2 \neq c_3$のケースでどうなるかを試してみよう)．

類似の方程式ロトカ・ヴォルテラの「競争」方程式があるので，その違いに注意する．