並列計算の基礎

コンピュータ上で何らかの計算を行う際，CPU(中央処理装置)の上では，一つの計算単位(スレッドと呼ぶ)が立ち上がって，そのスレッド上で必要な計算が順々に行われていきます．一方で並列計算では，プログラムから複数のスレッドを立ち上げて，それらのスレッドに別々の計算を同時にやらせることで，処理を効率化します．今回の講義ではOpenMPと呼ばれるライブラリを用いて並列計算の基礎について学びます．

OpenMPの基礎

事前準備

この講義では OpenMP と呼ばれる並列計算のライブラリを使います．CygwinやMSYS2を使っている場合には特に準備は必要ありません．Macを使っている場合にはHomebrewを導入後，ターミナルから

brew install libomp

とタイプしてOpenMPをインストールしておいてください．

準備が完了したら，以下のソースコードを適当な名前で保存し，コンパイル，実行してください．コンパイル方法はWindows (Cygwin) を使う場合と，Macを使う場合とで異なりますので注意してください．

ソースコード

print.c


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#include <stdio.h>

#ifdef _OPENMP
#include <omp.h>
#endif

int main() {
    #pragma omp parallel
    {
        #pragma omp single
        {
            printf("#threads: %d\n", omp_get_num_threads());
        }

        printf("Hello, world!\n");
    }

    #pragma omp parallel for
    for (int i = 0; i < 10; i++) {
        printf("%d\n", i);
    }
}

コンパイル

# Windows(Cygwin)を使っている場合
gcc print.c -fopenmp

# Macを使っている場合
gcc print.c -Xpreprocessor -fopenmp -lomp

Macを利用している場合，環境によっては -L/usr/local/opt/libomp/lib (少し古いHomebrew)や-L/opt/homebrew/opt/libomp/lib/ (新しいHomebrew)のようにライブラリの場所を指定する必要があるかもしれません (-lompの前に入れてください)．

実行結果

正しく実行できると，シェル上に以下のように表示されます (スレッドの数は環境によって異なります)．

#threads: 4
Hello, world!
Hello, world!
Hello, world!
Hello, world!
6
4
5
2
7
9
8
0
3
1

基本プログラムの解説

上記のような結果が得られることが確認出来たら，冒頭のプログラム (print.c)の内容を見ていきましょう．

3-5行目では今回並列計算に用いるライブラリであるOpenMPのヘッダファイルをインクルードしています．この時，開発環境にOpenMPが用意されているかどうかを，マクロ定義_OPENMPを用いて判定しており，OpenMPがある時にだけ，ヘッダをインクルードするようにしています．

このマクロ_OPENMPはOpenMPが使える場合には，そのバージョンが公開された日付を表す数字が入っています．例えば，201107であればOpenMP 3.1, 201511であればOpenMP 4.5といった具合です．この番号とバージョンの関係は，以下のWebページでチェックすることができます．

https://www.openmp.org/specifications/

8-16行目では，実行環境に何個の計算リソースが存在するのかを取得，プリントしています．ここでいう計算リソースはスレッドと呼ばれるもので，通常はCPUに$N$個のコアがある場合$2N$個までスレッドを同時起動できます (CPUの仕様によるため，1コアにつき1スレッドまでのものもある)．

OpenMPでは #pragma omp parallel というマクロを書いた後に{ }で括られた領域 (プログラムの8-16行目) が，利用可能な全てのスレッドで実行されます．そのため，先ほどの実行結果ではHello, worldがスレッドの数と同じ4回表示されています．

一方で #pragma omp parallel によって囲まれたセクションの中で，さらに #pragma omp single で囲まれたセクションを作ると，その部分は，1つの代表スレッドだけがその部分を実行し，その他のスレッドはその部分を無視します．そのため，スレッドの数の表示は一度だけしか行われません．

ここで用いられるスレッド数を取得する関数 omp_get_num_threads() は #pragma omp parallel の外で呼び出されると常に1を返すので，このような少し入り組んだ形で呼び出しています．

18-21行目ではfor文を並列に実行しています．for文を並列に実行したい場合には #pragma omp parallel forというマクロをfor文の直前に書けばよく，非常に単純です．for文が並列実行されるときには，まず最初にどのスレッドが何番目の内容，このプログラムで言えば0-9のどの値を担当するかを決めて，それぞれのスレッドがfor文の中身を同時に実行します．そのため，for文の内容がiの順序に関係なく実行されて，実際の実行結果から分かるように，番号が適当な順で出力されています．

なお，OpenMPはデフォルトでは，1回目のループ → 第1スレッド, 2回目のループ → 第2スレッド, …, n回目のループ → 第(n % スレッド数)スレッドというように処理の担当を決定します．この方式を並列計算の用語でラウンドロビン方式と呼びます．これはOpenMPでは明示的に以下のように書く場合と同じです．

#pragma omp parallel for schedule(static, 1)
for (int i = 0; i < 10000; i++) {
    ...
}

scheduleのカッコの中にの1つめスケジュールの方式で，staticは先ほど説明したラウンドロビン方式の割当を指します．これ以外にもいくつかのスケジュール方式がありますが，よく使うものだと，早いもの勝ちで処理が済んだ順から次のループの処理を実行していく dynamicというスケジュール方式があります．scheduleの2番目に指定されている数字は，担当を決めるときに，何個の連続したループを処理するかを表しています．もし2が指定されていれば，第1スレッドは1回目と2回目のループ，第2スレッドは3回目と4回目のループというより処理を行います．

OpenMPにより作成される各スレッドは，お互いが干渉することなく，独立に計算を進める事ができる一方で，メモリ上に格納されたデータは共有しています．従って，並列化がなされる前に用意したデータに対しては，複数のスレッドからアクセス可能です (以下の例を参照)．

int *data = (int*)calloc(10, sizeof(int));   // メインスレッドがメモリを動的確保

#pragma omp parallel for
for (int i = 0; i < 10; i++) {
    // 並列で動く別スレッドが上記のメモリにアクセス可能
    data[i] = i;
}

練習問題

print.c のプログラムを改良して，並列のfor文を使って1から10000の合計を計算するプログラムを作成せよ．ここでは，上記のプログラムを単純に拡張するだけでよく，正しく解が求まらないことを確認せよ．

排他制御

排他制御とロック

さて，上記の練習問題で正しく合計は計算できたでしょうか？おそらく，何度か実行すると正しい答えが得られる場合と，そうでない場合があったのではないでしょうか？

このように正しく和が計算できないことは普通にfor文を実行すれば起こりえないわけですから，当然，並列計算の影響により間違った結果が得られていると予想できます．先ほど述べた通り，並列計算を実行するスレッドの間ではデータが共有されているので，全てのスレッドは和を計算中に和の値を格納しておく変数にアクセスできます．データを読み取るだけであれば，それで問題がないのですが，データを書き込む場合には注意が必要です．

例えばプログラムが以下のように書かれているとしましょう．

int sum = 0;

#pragma omp parallel for
for (int i = 1; i <= 10000; i++) {
    sum += i;
}

あるスレッドが sum = sum + 1 を実行するときには，以下の順序で計算を行います．

sum から値を読み取る．
sum の値に1を足す．
sum に1を足した値を書き込む．

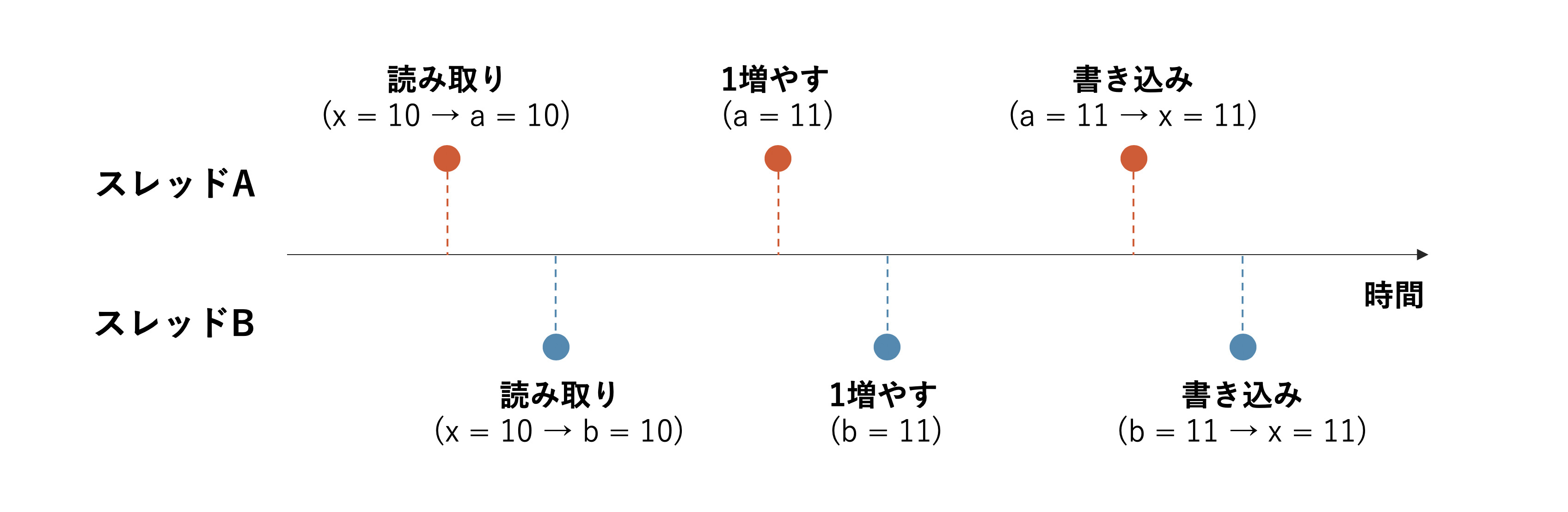
ここで問題になるのは，いくら計算が速いコンピュータであっても，1番の処理を実行してから，3番の処理を実行するまでには微小な時間の差があるということです．そのため，以下の図を見て下さい．

この図では，2つのスレッドAとBはほぼ同じタイミングで$x$に格納されている値(今回の場合は$x=10$)を読み取り，A, Bの各スレッドがそれぞれで管理するメモリ領域 (図ではこれらを$a$, $b$という変数で表した)に保存します．

各スレッドでは，この$a$, $b$を1ずつ増やしたあとで，スレッド間で共有された変数$x$にその値を書き込みます．従って，スレッドAが$x$を1増やした値を書き込む前に，スレッドBが$x$の値を読み取ってしまうと，本来2増えるべき値が1しか増えないということが起こってしまうのです．

これが，先ほどの計算において，正しい結果が得られなかった原因です．

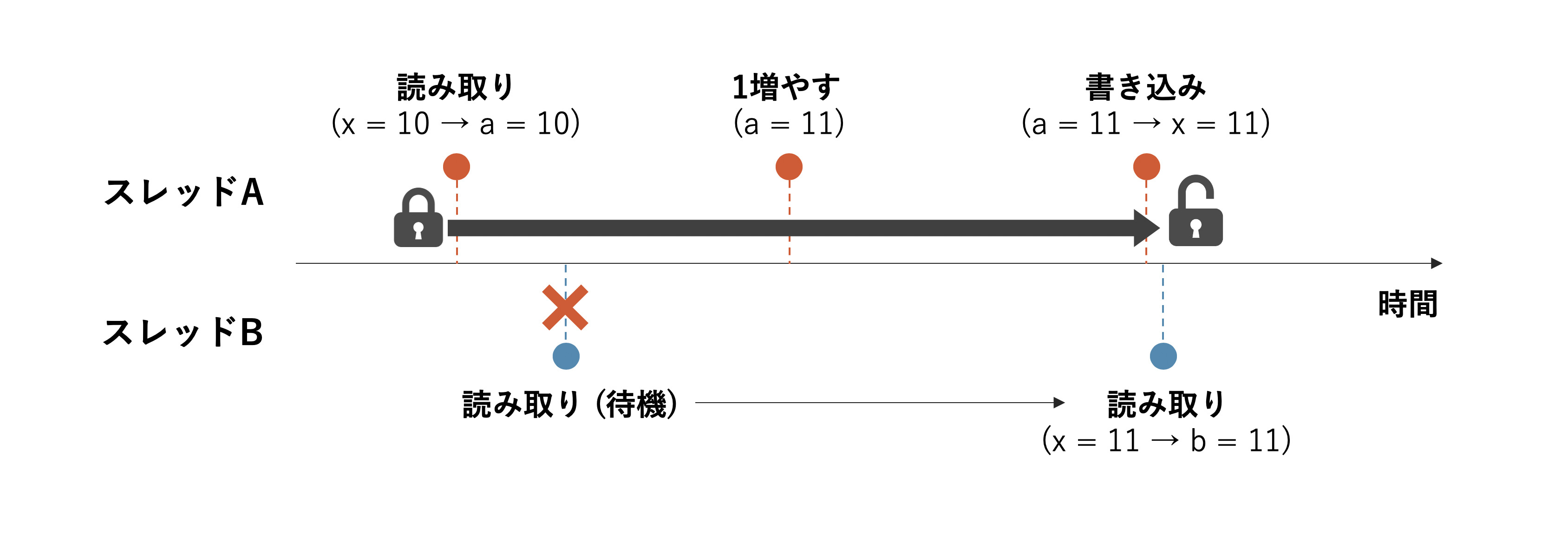
このような期待しない処理を防ぐための仕組みにロックがあります．ロックというのは，プログラム中のある処理を同時に1つのスレッドだけしか実行できないようにする仕組みです．ロックをはじめとした，単一のスレッドのみが特定の処理を実行するように制御する仕組みのことを排他制御と言います．上記の和の計算の例でいえば，1-3の一連の処理が1つのスレッドしか実行できなければ正しく和が計算できると期待できます．

それでは，実際にロックを使ってそれを確かめてみましょう．上記のプログラムをOpenMPのロックである omp_lock_t 型の変数を使って書き直してみます．

omp_lock_t lock;
omp_init_lock(&lock);

int sum = 0;

#pragma omp parallel for
for (int i = 1; i <= 10000; i++) {
    omp_set_lock(&lock);
    sum += i;
    omp_unset_lock(&lock);
}

OpenMPのロックは使用する前に omp_init_lock(omp_lock_t *) 関数を使って初期化をする必要があることに注意してください．初期化後は omp_set_lock(omp_lock_t *)でロックを設定し，omp_unset_lock(omp_lock_t *)でロックを解除します．

あるスレッドによってロックがかけられているときには，他のスレッドは omp_set_lock を実行するところで待機するようになります．そのため，もしロックの解除を忘れると，処理が進まずにプログラムが終わらなくなるので注意しましょう．

クリティカル・セクションとアトミック操作

上記のロックを用いることで和の計算を正しく計算できるようになりましたが，ロックを用いたプログラムはロックを解除し忘れる可能性があるなど，少々手間がかかります．

ロックは，複数のスレッドがお互いに通信しながら変数の読み込みや書き込みを行うような場合に有効ではありますが，単純なプログラムにおいては，より使いやすい仕組みが用意されています．それがクリティカル・セクションとアトミック操作です．

クリティカル・セクションとは直訳すれば「重要な場所」というような意味になりますが，言い換えれば，複数のスレッドが同時実行すると困る場所という意味です．これは先ほどロックを使って実現したものと同様，1つのスレッドだけがその領域を実行することを保証するもので，以下のように使用します．

int sum = 0;

#pragma omp parallel for
for (int i = 1; i <= 10000; i++) {
    #pragma omp critical
    {
        // 中括弧は改行して書かないといけない
        sum += i;
    }
}

こちらの方が，初期化やロック，アンロックの明示的な呼び出しがなく，プログラムがすっきりしています．また，実行結果についても，正しく和が計算できるはずです．

ここまでのロックとクリティカル・セクションはどちらも，一定の計算が単一のスレッドでのみ実行されることを保証するものでした．ですが，ロックやクリティカル・セクションはそれらの設定のために余計な計算処理が必要になるために，計算時間が増加します．

実際，上記のプログラムの実行時間を並列化なしと，クリティカル・セクションを用いたもので比較すると，クリティカル・セクションを利用したものが数倍遅くなっていることが分かるはずです (これを調べるのが後の課題です)．

今回の並列化においては，for文の中に並列で処理できない和の計算しか入っていないので，速くならないのは当然なのですが，それにしても，これだけ大幅に遅くなるのは問題と言えそうです．

一方で，足し算や掛け算のような単純な値の書き換えの場合にのみ利用できる，より軽量な排他制御の仕組みにアトミック操作があります．上記の和を計算するプログラムでは，排他制御したい処理は単純な和の書き込みなので，以下のようにしてアトミック操作に書き換えることができます．

int sum = 0;

#pragma omp parallel for
for (int i = 1; i <= 10000; i++) {
    #pragma omp atomic
    sum += i;
}

ちなみにアトミック操作という言葉それ自体は，ある操作ないし処理が，排他制御下で単一のスレッドだけで行われていることを指す用語であり，上記のomp atomicにより実現される物だけを指すわけではありません．

少し難しい話ですが omp atomic は sum += i のような計算に対して用意されたCPU上のハードウェア的なアトミック操作命令を呼び出しています．そのため，ソフトウェアのレベルで排他制御を行うロックやクリティカル・セクションよりも高速に動作します．その代わりCPUにアトミック操作の命令が用意されていなければならず，特定の処理にしか使えないのです．

課題1 (配点: 2点)

ここまでに紹介したロック，クリティカル・セクション，アトミック操作を利用した和の計算プログラムと並列化を用いない単純な和の計算プログラムを作成し，それぞれの実行速度を比較せよ．

なお，比較にあたってはint等の整数型に対する計算だと差が見えづらいので，double型の値の和を取ることを考えたい．単に，ランダムな値を足すだけでも構わないのだが，ここでは整数の二乗の逆数の和が$\frac{\pi^2}{6}$に収束することを利用して，円周率の値を求めてみよう．

並列化を用いない関数は以下のようになるので，これを適宜コピーして，ロック等の処理を加えた関数を作成せよ．なお，OpenMPで並列計算をしている場合の計算時間の測定はtime.hのclock()関数ではなく，OpenMPが提供しているomp_get_wtime()を用いる．

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <omp.h>

double calc_pi_simple(int n) {
    double sum = 0.0;
    for (int i = 1; i <= n; i++) {
        sum += (1.0 / i) / i;
    }
    return sqrt(sum * 6.0);
}

int main(int argc, char **argv) {
    // 項数の初期値は1000とし，適宜コマンドライン引数から項数を読み取る
    int N = 1000;
    if (argc > 1) N = atoi(argv[1]);

    double pi, start, end;

    // 時間を計測しながら処理を実行する
    start = omp_get_wtime();
    pi = calc_pi_simple(N);
    end = omp_get_wtime();
    printf("Pi (w/o parallel): %.12f\n", pi);
    printf("Time: %f ms\n", 1000.0 * (end - start));
}

なお，上記のプログラムではコマンドライン引数に

./summation 1000000

のように整数を指定することで，和を取る項の数を変更することができる．適宜，和を取る項数を変化させて，計算時間の違いを観察すると良い．

リダクション処理の並列化

ここまで，様々な排他制御のやり方を説明するために和の計算プログラムを作ってきましたが，これらは並列計算の仕組みを上手く利用しておらず，for文の中身が常に単一のスレッドで実行されるために，並列計算なしで和を計算するのと比べて効率化できたとは言えませんでした．

上記のプログラムでは$1 + \frac{1}{2^2} + \frac{1}{3^2} + \cdots$のように数列の和を取っていました．このように，とある数列に対して，同じ演算子を次々に適用していき，1つの答えを求めるような操作をリダクション処理と呼びます．

このようなリダクション処理の場合には，分割統治法 (divide and conquer)と呼ばれる考え方を使って，処理を高速化することができます．

分割統治法

これまでのプログラムでは，複数のスレッドが答えが格納される単一の変数 (上記の円周率を求めるプログラムならsum)に対して値を足し算しているがために，足し算が行われる際に変数をロックする必要がありました．

ですが，各スレッドが自由にアクセスできる変数を別々に用意していれば，上記のロックを減らすことができそうです．

今，仮にスレッドが4つあるとして，第1000項までの和を取りたいとするなら，第1スレッドが第1-250項，第2スレッドが第251-500項，第3スレッドが第501-750項，第4スレッドが第751-1000項の和を担当(＝分割統治)することにして，最後に4つのスレッドが別々に求めた4つの数を足し算すれば，正しく全体の和が求まりそうです．

そこで，最初のprint.cのプログラムを参考に，次のような利用可能なスレッド数を取得する関数を用意しておきます．

int get_num_threads() {
    int ret = 1;
    #pragma omp parallel
    {
        #pragma omp single
        {
            ret = omp_get_num_threads();
        }
    }
    return ret;
}

この関数を利用して，スレッド数と同じ要素数を持つ配列を動的確保し，その配列の各要素に対して，各スレッドが独立に和を計算できるようにします．

#define max(a,b) (((a) > (b)) ? (a) : (b))
#define min(a,b) (((a) < (b)) ? (a) : (b))

int main(int argc, char **argv) {
    int N = 1000;
    if (argc > 1) N = atoi(argv[1]);

    // スレッド数を取得
    const int num_threads = get_num_threads();

    // 各スレッドが担当するセクションの長さ
    // (配列サイズがスレッド数で割り切れない場合を考慮)
    const int section_size = (N + num_threads - 1) / num_threads;

    // 和を求める
    double sum = 0.0;

    #pragma omp parallel for
    for (int t = 0; t < num_threads; t++) {
        const int start = section_size * t + 1;
        const int end = min(section_size * (t + 1), N);
        double part_sum = 0.0;
        for (int i = start; i <= end; i++) {
            part_sum += (1.0 / i) / i;
        }

        #pragma omp atomic
        sum += part_sum;
    }

    printf("Pi (d&c): %.12f\n", sqrt(sum * 6.0));
}

OpenMPによる組み込みリダクション操作

OpenMPには，上記の分割統治法と同じように，複数のスレッドが干渉しないようにリダクション操作を行う仕組みが用意されています．

この操作はomp parallel forと組み合わせて利用され，リダクションの結果を格納する変数と，その変数に対して行うリダクション操作を以下のような形で指定します．

double sum = 0.0;
#pragma omp parallel for reduction(+:sum)
for (int i = 1; i <= N; i++) {
    sum += (1.0 / i) / i;
}

すると，プログラムの内部ではsumがfor文の中に入る前に各スレッド上にコピーされ，スレッド内では別々のsumを使って独立に加算操作を行います．

for文から抜けるときには，各スレッドの計算結果が改めて，共有されているsumに対して加算されるというものです．

なお，このreduction操作に指定する演算は初期状態では+や*などの二項演算に加え，(OpenMP 3.1以降では) maxやminなどの操作を指定できます．なお，OpenMPのバージョンを調べる場合には，以下のようにしてバージョン番号を表す数字をチェックすると良いです．

printf("%d\n", _OPENMP);

この数字が 201107 よりも最近の日付を表す数字になっていれば，OpenMPのバージョンは3.1以上です．

課題2 (配点: 2点)

上記の説明を参考に，分割統治法とOpenMPのreductionを使った円周率計算のプログラムを課題1で作成したプログラムに追加し，これらの実行速度を比較せよ．

ここまでの結果は，和を取る項の数を$10^6 – 10^7$程度に設定すると，速度の違いが分かりやすい．和を取る項の数は上記の通りコマンドライン引数から指定可能である．

./summation 1000000

デッドロック

OpenMPを用いる，用いないに関わらず，並列計算や並行計算 (各スレッドが異なる処理を同時に行う計算法)では，デッドロックと呼ばれる問題が起こる可能性があります．

これは，ここまでで解説してきた排他制御に関係する問題で，実行中の複数のスレッドが，これまた複数の変数(リソース)へのアクセスを待機するようにした結果，お互いが必要なリソースをロックしてしまって，処理が完全に停止してしまうことを指します．

例えば，スレッドAとスレッドBが処理を実行する際に2つの異なるリソースPとQの両方を必要とするケースを考えてみましょう．

スレッドAがPをロックするのと，ほとんど同時にスレッドBがQをロックすると，スレッドAはQへのアクセスを待機し，スレッドBはPへのアクセスを待機します．スレッドAとスレッドBはお互いに処理を実行するまではP, Qのロックを解除しませんので，結果として，2つのスレッドともに待機状態になってしまい，処理が完全に停止してしまいます．

この状態に陥ってしまう問題の典型例として，「食事をする哲学者」 (dining philosophers)という問題が知られています．この問題は以下のようなものです．

食事をする哲学者の問題

哲学者が4人(人数は任意でよい)，円形のテーブルに腰掛けている．この哲学者たちは考え事をしながら，テーブルの中心にあるスパゲティを食べている．このスパゲティは麺が絡み合っているため，これを口に運ぶためにはフォークを2本使う必要がある．

フォークは4人の哲学者の間に，それぞれ1本ずつおいてあり，各哲学者は自分の両隣にある2本のフォークの両方を手にすることで初めてスパゲティを食べることができる．ところが，哲学者は考え事をしているため，一度手にしたフォークはスパゲティを口に運ぶまで離さない．

彼らはお腹いっぱいスパゲティを食べることができるだろうか？

この問題において，例えば4人の哲学者全員が自分の右手側にあるフォークを取ったとしましょう．彼らは全員，考え事をしており，右手に取ったフォークを離すことはありませんが，その一方で，左側のフォークは左隣に座っている哲学者によって，すでに取られています．

結果として，哲学者たちは永久に2本のフォークを取ることができず，デッドロック状態に陥ってしまうというわけです．

この問題をC言語を用いて実装したものを以下に用意しました．

philosopher.c


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

#include <stdio.h>
#ifdef _OPENMP
#include <omp.h>
#endif

typedef struct {
    int user;
    omp_lock_t lock;
} fork;

void init_fork(fork *f) {
    f->user = -1;
    omp_init_lock(&f->lock);
}

void pick_fork(fork *f, int who) {
    omp_set_lock(&f->lock);
    f->user = who;
    omp_unset_lock(&f->lock);
}

void put_fork(fork *f) {
    omp_set_lock(&f->lock);
    f->user = -1;
    omp_unset_lock(&f->lock);
}

#define N 5
#define FULL 10
int count[N];
fork forks[N];

int main() {
    for (int i = 0; i < N; i++) {
        count[i] = 0;
        init_fork(&forks[i]);
    }

    for(;;) { 
        #pragma omp parallel for
        for (int i = 0; i < N; i++) {
            // i: 1本目のフォークの番号 (=哲学者の番号)
            // j: 2本目のフォークの番号
            int j = (i + 1) % N;
            if (count[i] != FULL) {
                // 1本目のフォークを誰かが使っているか？
                if (forks[i].user == -1) {
                    // 使っていなかったらフォークを取る
                    pick_fork(&forks[i], i);
                }

                // 2本目のフォークを誰かが使っているか？
                if (forks[j].user == -1) {
                    // 使っていなかったらフォークを取る
                    pick_fork(&forks[j], i);
                }

                // 2本のフォークを持っているか？
                if (forks[i].user == i && forks[j].user == i) {
                    // 持っていたら食事をする
                    printf("Eating: %d\n", i);
                    count[i] += 1;

                    // 一旦持っているフォークを離す
                    put_fork(&forks[i]);
                    put_fork(&forks[j]);
                }
            }
        }

        // 全員のお腹がいっぱいになっているか？
        int success = 1;
        for (int i = 0; i < N; i++) {
            if (count[i] != FULL) {
                success = 0;
            }
        }

        // 全員お腹がいっぱいなら終了
        if (success == 1) {
            break;
        }
    }
    printf("Finish!\n");
}

まずは，状況を確認するために，このプログラムをコンパイルして実行してみましょう．このプログラムでは，各哲学者が10回ずつスパゲティを口にすると，満足して食事をやめるようになっています．

試しに何度か実行してみると，プログラムが途中で停止してしまい，最後まで実行できないことが確認できると思います．

デッドロックの解消法

デッドロックを防ぐ方法には，いくつもの方法がありますが，もっとも分かりやすいものは，もし処理の実行に必要なリソースを全て取得することができなければ，ロックしたリソースを一度解放する，というものです．

食事をする哲学者の問題で言えば，もし哲学者が1本だけフォークを手にとったものの，2本目のフォークを取ることができなかった場合，先に手にとった1本目のフォークをテーブルに戻すようにします．

もちろん，このやり方でも，全ての哲学者が完全に同調した動きで，右のフォークを取る，左のフォークが取れるかをチェック，左のフォークが取れずに右のフォークを離す，ということを繰り返すと，永遠にスパゲティを食べることはできません．

しかしながら，計算機上の処理では，このような完全な同調が起こることは非常に稀であるため，上記の解決策が十分に上手く動作します (今回は必要なリソースが2つなので上手くいくが，より多くのリソースを同時に必要とする場合は，これだけでは不十分)．

課題3 (配点: 2点)

上記のデッドロックの解消法を参考に「食事をする哲学者」のプログラム philosopher.c をデッドロックが起こらないように改良せよ．

多重ループの並列化

ここまでのプログラムでは，単一のforループを並列化する場合について考えてきましたが，これまでの講義で扱った内容には，行列同士の掛け算のように多重ループを伴う計算も少なくありません．

このような多重ループを伴う計算においてはどのような並列化を行うのが適切なのかを考察してみましょう．以下のプログラムは，行列の掛け算のプログラムの一部を切り出したものです．

for (int i = 0; i < res->rows; i++) {
    for (int j = 0; j < res->cols; j++) {
        mat_elem(temp, i, j) = 0.0;
        for (int k = 0; k < mat1.cols; k++) {
            mat_elem(temp, i, j) += mat_elem(mat1, i, k) * mat_elem(mat2, k, j);
        }
    }
}

この部分にはforループが3つ含まれていますが，どのループを並列化するのが最も効率的でしょうか？あるいは，複数のループを並列化してもよいのでしょうか？

まず，基本的にOpenMPの並列化はループがネストしないように呼び出さなければなりません．つまり，上記のような三重ループであれば，3つのforループの中で1つだけを並列化するようにします．

次に，3つの中でどれを並列化するかという点についてですが，最も内側のkに関する計算は和の計算であり，(リダクション操作など工夫の余地はあるものの)完全には並列化できないので，効率はそれほど良くなさそうです．

一方で，上記の行列積の計算は各i, 各jに関しては完全に独立した計算になっていることに気づきます．従って，iかjかどのどちらかを並列化すればよいのですが，一般的には外側のループであるiでのforループを並列化します．

これは，並列のforループが始まるときには新しいスレッドを作ったり，データをコピーしたりといった余計な処理が必要となるためで，このような余計な処理をする回数を減らすためにも，最も外側のループを並列化するのが良いとされています．

ただ，これはあくまで内側の処理が完全に独立実行可能である場合に限るため，常に一番外側のループを並列化しておけばよいわけではないことに注意して下さい．練習として，行列積とガウスの消去法を並列化する課題に取り組んでみましょう．

課題4 (配点: 4点)

対称行列 (エルミート行列でも良い)の固有値を計算する方法の一種にべき乗法という方法が知られています．これはとある正方行列$\mathbf{A}$の最大固有値と，その固有値に対応する固有ベクトルを求める方法です．

べき乗法はランダムなベクトル$\mathbf{x}_0$を用意し，次のように$\mathbf{x}_k~~(k=0, 1, 2, \ldots)$を更新していきます．

\[\begin{aligned} \mathbf{y}_k &= \mathbf{A} \mathbf{x}_{k - 1} \\ \mathbf{x}_k &= \mathbf{y}_k / \| \mathbf{y}_k \| \end{aligned}\]

すると十分大きな$k$に対して$\mathbf{x}_k$は行列$\mathbf{A}$の「絶対値が最大となる固有値」に対応する固有ベクトルとなります．従って，この固有ベクトルに対応する固有値は以下のように求めることができます (今回の計算では常に$\mathbf{x}$の長さが1に正規化されているので分母の計算は必ずしも必要はない)．

\[\lambda = \frac{\mathbf{x}_k^T \mathbf{A} \mathbf{x}_k}{\mathbf{x}_k^T \mathbf{x}_k}\]

また，これと対となる方法に逆べき乗法というアルゴリズムがあり，これはべき乗法とは反対に，最小の固有値と，最小固有値に対応する固有ベクトルを求める方法です．

逆べき乗法では，$\mathbf{x}_k$を次のように更新していきます (単なる$\mathbf{A}$の掛け算が逆行列の掛け算になっている)．

\[\begin{aligned} \mathbf{y}_k &= \mathbf{A}^{-1} \mathbf{x}_{k - 1} \\ \mathbf{x}_k &= \mathbf{y}_k / \| \mathbf{y}_k \| \end{aligned}\]

逆べき乗法は行列$\mathbf{A}$の逆行列の固有値が，元の行列$\mathbf{A}$の固有値の逆数となることを利用しています．また，このとき，固有値に対応する固有ベクトルの値は変化しません．

すると，べき乗法によって固有値の逆数$1 / | \lambda |$が最大となるような固有値$\lambda$が求まるため，結果として元の行列$\mathbf{A}$が正則(逆行列がある＝固有値に0がない)である場合に限り，固有値の中で絶対値が最小な固有値が求まります．

上記の計算では，行列の掛け算ならびに線形問題を解く計算を繰り返し行う必要があるため，1回の計算にかかる時間を短縮することは非常に重要です．そこで，行列の掛け算と線形問題を解く処理を並列化して処理を効率化しましょう．(逆べき乗法を使うときには，逆行列を先に求めたり, LU分解してしまうほうが圧倒的に効率的だが，今回は練習のためにあえて非効率的な方法を使う)

以下のURLからダウンロードできるテンプレート・プログラムにべき乗法ならびに逆べき乗法を実装し，並列化の有無によって，計算時間がどのように変化するかを調べてください (プログラム内では500x500の行列の固有値を求めています)．

テンプレート・プログラム (power.zip)

課題の作成方法

上記のテンプレート・プログラムをダウンロードして展開したら，これまでに作成してきたmatrix.cならびにmatrix.hをフォルダ内にコピーして下さい．

まずは，ZIPファイルに含まれていたpower.cにべき乗法と逆べき乗法を実装します．このプログラムを実行すると，最初に$2 \times 2$の小さな行列に対してテストが動きます．入力の行列と，その固有値，固有ベクトルは次のようになります．

\[\begin{aligned} \mathbf{A} &= \begin{pmatrix} 1 & 3 \\ 3 & 1 \end{pmatrix} \\ \lambda_0 &= 4, \quad \lambda_1 = -2 \\ \mathbf{u}_0 &= \begin{pmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{pmatrix}, \quad \mathbf{u}_1 = \begin{pmatrix} \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} \end{pmatrix} \end{aligned}\]

また，今回のプログラムでは，乱数のシード (コンピュータ上で疑似乱数の生成に使うパラメータ)を固定してあるため，500x500のランダム行列についても得られる最大・最小固有値は以下の値に固定されています．

\[\lambda_0 = 249.97410179, \lambda_{N-1} = -0.03985054\]

正しい値が計算できることが確認できたら，コピーしてきたmatrix.cをOpenMPで並列化して書き直します (mat_mulとmat_solveだけ更新すれば良い)．

プログラムが完成したら，並列化の有無による計算量の違いを調べるため，プログラムを呼び出すときにOMP_NUM_THREADSという環境変数に使用するスレッド数を指定して下さい．

# 通常通りの呼び出し (使えるだけスレッドを使う)
./power                     
# 並列化なし (1スレッドしか使わない)
OMP_NUM_THREADS=1 ./power

スレッドが4つある環境下では，べき乗法が3倍程度，逆べき乗法が2倍程度高速化されるはずです．