近似・補間
目次
今回の講義では離散的なデータを連続的な関数により近似・補間する方法について学びます.今回作成するプログラムでは前々回までで作成したmatrixライブラリを使用しますので,前回課題ができていない人は,以下のZIPファイルをダウンロードして使ってください.
前回までのレポートをこのファイルで提出するのはやめましょう
ライブラリの作成
今回は,近似・補間の話題に入る前に,C言語におけるライブラリの作成方法について学びます.
これまでは実行可能なプログラムを得るために,全てのソースコードが揃っている必要がありました.ライブラリはほとんど変わることがないソースコードを予めコンパイルしてまとめたもので,ライブラリを作成しておくと,ソースコードがなかったとしても,ライブラリを持っているだけでそのプログラムの内容を再利用できます.
このようなライブラリの考え方は,プログラム内容を他人と共有する場合に,ソースコードが多かったり,そもそもソースコードの中身を見せたくない場合に役立ちます.
ヘッダファイルのインクルードについて
#include や #define などの # で始まるコマンドは,プリプロセッサと呼ばれます.プリプロセッサは,preprocess(=前処理)の指示をするためのコマンドで,これらのコマンドの指示は,コンパイル作業を行う直前にコンパイラにより自動的に実行されます.
例えば,#define というのは,置き換えを定義するプリプロセッサです(実際には,置き換え以外の使い方もあります).プログラム冒頭で,
#define AAA 3
と書いておくと,コンパイル直前に,ファイル中の AAA という部分が,まず3に置き換えられ,その後,コンパイル作業が始まるというわけです.
このような「置き換え」を行うのはヘッダファイルの場合も同様です.例えば,
#include <filename>
というプリプロセッサは,コンパイルに先立ってfilenameで指定されたファイルを,ソースファイル中に取り込む(別の言い方をすれば #include <filename> の部分が,filename のファイルの中身で置き換えられる)という働きを持ちます.このとき,
#include <stdio.h>
のように,ファイル名が < と > とで囲まれている場合には,コンパイラは,あらかじめ定めてある標準的なディレクトリ(例えば /usr/local/include など)から,該当するファイルを探し出します.一方で,
#include "matrix.h"
などのように,ファイル名をダブルクオーテーションで囲った場合には,当のソースファイルがあるディレクトリから順に,ファイルの探索を行います.
したがって,C言語の標準ヘッダファイルをインクルードするときは <xxx.h> の表記を用い,自分で作ったヘッダファイルをインクルードする場合には "xxx.h" の表記を用いる場合が一般的です.
ヘッダファイルの書き方
前回の課題で,matrix.h というヘッダファイルを作成しました.サンプル通りに matrix.h を作成した場合,ファイル冒頭に,
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
という形で,3つの標準ヘッダファイルをインクルードするようになっているはずです.
一方,サンプルの main.c においては,
#include <stdio.h>
#include "matrix.h"
として,stdio.h と matrix.h とをインクルードしているはずです.さて,#include というプリプロセッサは,該当部分を指定されたファイルの内容で置き換える働きをするので main.c における #include matrix.h の部分を実際に置き換えてみると,main.c の冒頭部分は,
#include <stdio.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
となります.
置き換わった結果を見ると一つ気になることがあります.ヘッダファイル stdio.h は main.c と matrix.h の両者でインクルードされていたため,上記のように置き換えて考えると,stdio.h がだぶってインクルードされてしまっています.
では,ヘッダファイルを二重にインクルードしてしまうとどうなるのでしょうか?試しに,
#include "matrix.h"
#include "matrix.h"
int main() {
return 0;
}
というサンプルプログラムをコンパイルしてみると matrix.h の中の全ての宣言に対して,次のようなエラーが大量に発生します(実際に,やってみてください).
matrix.h:14: conflicting types for `mat_alloc'
matrix.h:14: previous declaration of `mat_alloc'
これは,matrix.h を2回インクルードしたために,matrix.h 中にある宣言が,すべて2回ずつ行われてしまい,結果として「宣言が重複している」というエラーが発生しているのです.
では次に,標準ヘッダファイルである stdio.h をダブってインクルードしてみます.
#include <stdio.h>
#include <stdio.h>
int main() {
return 0;
}
というサンプルプログラムをコンパイルしてみましょう.すると,今度は,何もエラーが発生せずにコンパイルが終了します.これは,なぜなのでしょうか?
実は,標準ヘッダファイルには,2度以上インクルードされても問題が発生しないように,ある工夫がされています.例えば,/usr/include/stdio.h の中身をのぞいてみると,冒頭のコメントに続いて,
#ifndef _STDIO_H
#define _STDIO_H
と書かれています(環境によっては,途中に余計な行が混じってる場合もあります).この #ifndef _STDIO_H と #define _STDIO_H が(それと,ファイルの最後にある #endif が),重複インクルードをさける役割を果たしています.
#ifndef _STDIO_H
というのは,_STDIO_H というマクロが定義されていなければ(ifndef = if not defined),次の行から #endif が現れる行までをソースコードに残し,反対にマクロが定義されていれば,#endifまでの内容を無視しなさいい,という意味の命令です.そのため,ヘッダファイル全体を,
#ifndef _STDIO_H
#define _STDIO_H
// ヘッダファイル本体
#endif
というように,記述しておくと,
- 一度目にインクルードしたときには,
_STDIO_Hという名前のマクロが定義されていないため,全体が無事にインクルードされる.また,同時に,_STDIO_Hというマクロが定義される. - 2度目以降にインクルードされたときには,すでに
_STDIO_Hマクロが定義されているため,#ifndef 〜 #endif までのヘッダファイル本体は無視される.
という具合にして,多重にインクルードされた場合でも,ヘッダファイル中の定義が重複するのを防ぐことができます.以上が,標準ヘッダファイルにおけるエラー防止のからくりです.
さて,この方式では,マクロ名(上記の例では,_STDIO_H)の選定が重要です.このマクロ名は,どのような名前でも良いのですが,万一,ユーザーが定義するマクロ名や,他のヘッダファイルが用いるマクロ名と名前が重複してしまうと,上記のからくりが正しく動作してくれません.
そこで,マクロ名の重複を防ぐため,ヘッダファイル名に由来したマクロ名をつけることが良く行われます.上記の例では,stdio.hというファイル名をもとに,_STDIO_H というマクロ名を設定しています(ドット (".") はマクロの中に使えないため アンダースコア ("_") で置き換えています.また,ユーザが定義するマクロと万が一にも重複しないように,"_"(アンダースコア)を1つ(場合によっては複数個)マクロ名の冒頭につけています).
そこで本講義でも,上記の例に従って _MATRIX_Hというマクロ名を使って matrix.h を多重インクルードに耐えられるよう改良してみましょう.
ライブラリの種類
ライブラリというのは,良く使う関数を一つのファイルにまとめたもので,リンク時にライブラリを指定することで,ライブラリの中の関数が利用できます.ライブラリを作るのには一手間かかりますが,一度作ってしまえば,毎回分割コンパイルするより楽にmatrix.cの中身を再利用できます.
C言語をコンパイルすることで得られるライブラリには「静的リンクライブラリ」と「動的リンクライブラリ」の二種類があります.これらは,各オペレーティング・システムごとに,おおよそ以下のような名前付けのルールに従ったファイル名を持っています.
| OS | 静的 | 動的 |
|---|---|---|
| Windows | abcdef.lib | abcdef.dll |
| Mac OS | libabcdef.a | libabcdef.dylib |
| Linux | libabcdef.a | libabcdef.so |
なお,Windows上でCygwinやMsys2などを使っている場合,これらの環境はUNIXをベースとしているため,上記の表ではLinuxと同様の名前付けのルールに従います.
ライブラリの種類における「静的」と「動的」は,そのライブラリに含まれる関数を別のプログラムで利用する際に,コンパイル (より厳密にはリンク)の処理が必要か,そうでないかを表しています.
「静的」リンクライブラリは,プログラムがコンパイルされる時にその処理内容が決定している,という意味で「静的」であり,仮にライブラリの内容が変わった場合には,プログラム全体をコンパイル (より厳密にはリンク)し直す必要があります.
一方で「動的」リンクライブラリは,ライブラリ自体のコンパイルと,そのライブラリを利用するプログラムのコンパイルを切り離すことができ,ライブラリの内容が変わった場合には,ライブラリ側だけを再コンパイルすれば,プログラムを動かすことが可能です.
静的リンクと動的リンクを比較すると,静的リンクの方が,余計なファイル (たくさんの動的リンクライブラリ)を共有する必要がなく,単にプログラムさえ渡せば,実行できるというメリットが有ります.一方で,動的リンクはソースコードの改変時にライブラリだけを再コンパイルすればよい分,開発効率が良く,また複数のプログラムが共通の処理を行う場合などは,動的リンクの方が向いていると言えるでしょう.
静的リンクライブラリの作成
matrix.hとmatrix.cを簡単に再利用できるように,静的リンクライブラリを作成します.次の通りに作業をしてください.
- 自分の作業しているディレクトリに
matrix.hとmatrix.cがあることを確認 - その作業ディレクトリに
includeというディレクトリとlibというディレクトリを作成 -
matrix.hを,作成したincludeディレクトリに移動(もしくはコピー) -
matrix.cをコンパイル後,ライブラリ化 (以下を参照)
# 作業ディレクトリ内で作業しているとする
gcc -c -I./include matrix.c
ar rv ./lib/libmatrix.a matrix.o
ar というのが,Unixにおいてライブラリ作成を行うコマンドです(archive の略).その後に続く rv というのは ar コマンドのオプションで新規のライブラリ作成を意味します.オプションの詳細は,ar コマンドの man ページを見てください.
以上で,作業終了です.これで,lib ディレクトリの中に libmatrix.a というライブラリファイルができたはずです.ライブラリの詳しい話は割愛しますが,一般にライブラリファイルは libXXXXX.a というように,頭に lib がつき,拡張子は .a となります(UNIX/Linux系のシステムの場合).
ライブラリを利用する際には,コンパイルするときのオプションに -lXXXXX と書きます(XXXXXの部分にライブラリ名が入ります.例えばmatrixライブラリを使ってmain.cというファイルをコンパイルする場合のコマンドは gcc -lmatrix main.c となります).詳しくは,以降の課題のMakefileを見てください.
課題1 (配点: 2点)
前回作成した matrix.h を,多重インクルードに耐えられるようにし,上記の作業手順に従って matrix.c をライブラリ化せよ.
正しくライブラリが作成できているかを確認するため,以下のファイルを展開したもの(mylibというフォルダが出てくる)を上記の作業ディレクトリ(includeやlibと同じ階層)に配置し,mylibディレクトリ内でmakeを実行せよ.つまり,作業ディレクトリ内には
includelibmylib
の3つのフォルダがある状態になっている必要がある.
テスト用ファイル: mylib.zip
このZIPファイルにはテスト用の check_mylib.c と以下の内容の Makefile が含まれている.
CC := gcc
SRC := check_mylib.c
OBJ := check_mylib.o
DEP := check_mylib.d
CFLAGS := -O2 -Wall -I../include -MP -MMD
LDFLAGS := -L../lib -lmatrix
PROGRAM := mylib
.PHONY: all
all: $(PROGRAM)
$(PROGRAM): $(OBJ)
$(CC) -o $@ $^ $(LDFLAGS)
%.o: %.c
$(CC) -c $(CFLAGS) $< -o $@
-include $(DEP)
.PHONY: clean
clean:
rm -f $(OBJ) $(DEP) $(PROGRAM) $(addsuffix .exe,$(PROGRAM))
シェル (Cygwin) から make を実行することでコンパイルが行われるので,正しくコンパイルされるかを確かめる.なお Makefile から分かる通り,コンパイルにより生成されるプログラムの名前を a.out ではなく mylib にしているので注意すること.実行方法は ./a.out と書いていた時と同様で ./mylib とすれば実行できる.
動的リンクライブラリの作成
動的リンクライブラリについては,簡単なソースファイルを用意して,その動作を確認してみます.まずは,以下の3つのソースファイルを適当なディレクトリに作成してください.
greet.h
#ifndef _GREET_H
#define _GREET_H
void greet();
#endif
greet.c
#include "greet.h"
#include <stdio.h>
void greet() {
printf("Hello\n");
}
main.c
#include "greet.h"
int main() {
greet();
}
これを,以下のようにコンパイル・実行していきます.
# 動的リンクライブラリの作成 (Mac, Linux)
gcc --shared -o libgreet.so greet.c
# 動的リンクライブラリの作成 (Windows=Cygwin, MSYS2)
gcc --shared -o greet.dll greet.c
# mainのコンパイル
gcc -L./ -lgreet -o main main.c
# プログラムの実行
./main
するとgreetという関数が呼び出されて,「Hello」という文字が出力されるはずです.
次に,ライブラリのprintfに渡されている挨拶の内容を適当なものに変更します.例えば,
greet.c
#include "greet.h"
#include <stdio.h>
void greet() {
printf("Bonjour\n");
}
のように変更したとしましょう.上記の説明にある通り,動的リンクライブラリは「ライブラリだけ」を再コンパイルすれば動作が変わるはずですので,以下のようにライブラリの再コンパイルとプログラムの再実行をしてみます.
# ライブラリの再コンパイル
gcc --shared -o libgreet.o greet.c
# プログラムの実行 (プログラムは再コンパイルしなくて良い)
./main
すると,今回はプログラムを再コンパイルしていないにも関わらず「Bonjour」と出力されたはずです.このことから,動的リンクライブラリがプログラム自体の再コンパイルを必要としないことが分かります.
その代わり,動的リンクライブラリに依存するプログラムを実行する場合には,必ず動的リンクライブラリが存在している必要があり,上記の例で言えばmainを実行するためにはlibgreet.soファイルが必ず存在していなければなりません.
# 試しにライブラリを削除
rm libgreet.so
# プログラムの実行 (失敗することを確認する)
./main
近似
ここからが本日の本題となる離散データの近似と補間の内容です.
前置きが長くなりましたが,本日の本題である近似ならびに補間についての話題に入ります.これらは,与えられたデータ列,例えば離散的な時刻 $t_1, t_2, \ldots, t_n$ で観測された対象の位置 $x_1, x_2, \ldots, x_n$ に対しての処理ですが,出力となるデータの性質が異なっていることに注意が必要です.
近似はデータ列がどのような性質の関数$x(t)$かが分かっている場合に用います.例えば $x(t) = at^2 + bt + c$ であるなら,データ列の情報から未知のパラメータ $a, b, c$ を求めるのが近似です.
補間はデータ列が真の関数の値を忠実に表していて $x_i = x(t_i)$ であることは分かっているものの,サンプルされていない点,例えば $(t_i + t_{i+1}) /2 $などにおける$x(t)$の値が未知である場合に用います.補間では,何らかの (多くの場合,滑らかな) 関数をデータ列から求め,サンプルされていない場所における関数の値を得ます.
それでは,まず,近似から見ていきましょう.
近似のための評価関数
有限個の離散点 $x_1, x_2, \ldots, x_n$と,その点における関数値を表した観測値 $y_1, y_2, \ldots, y_n$ が与えられているとします.この時,$y$ が $x$の関数であるとして $y = f(x)$ に近い関数を見つけるのが近似です.この際,導入で述べた通り,関数 $f$ の形 (例えば,一次関数であるとか二次関数であるとか) は既知であるとし,その関数を実際に定義するのに必要なパラメータを求めていきます.
このパラメータを求めるためには,結果として得られる関数と,観測データができる限り近くなっている必要があります.そのため,この近さを測る指標が必要になってきます.
最も一般的には,関数の値と観測値の差の二乗,すなわち \(e(x_i) = ( f(x_i) - y_i )^2\) によって誤差を定義します.この誤差の定義を二乗誤差と言います.この誤差を全ての点 $x_i$ で合計した誤差を最終的な誤差とします.
\[E = \sum_{k=1}^{n} \left( f(x_k) - y_k \right)^2\]一例として,関数 $f$ が二次関数だと考えると $E$ は関数の未知パラメータ $a, b, c$ の関数 $E(a, b, c)$だと考えられます.この時 $E$ を最小にするような $a, b, c$ を数学的に以下のように書きます.
\[\{ a, b, c \} = \underset{a', b', c'}{\text{argmin}} ~E(a', b', c')\]今 $E$ は $a, b, c$ の関数であることが分かっていますので,数値的にあるいは数学的な計算の結果として $a, b, c$ がどのような値になるのかを定めることができます.この際,関数と観測値の近さを表わした関数 $e$ はある程度自由に決めることができます.最適化計算や機械学習などの分野では $\delta = f(x_k) - y_k$ として,以下のような関数がよく使われます.
絶対誤差
\[e(\delta) = | \delta |\]二乗誤差
\[e(\delta) = \delta^2\]フーバー損失 (Huber loss)
\[e(\delta) = \begin{cases} \frac{1}{2} \delta^2 & ( \delta < c ) \\ c ( | \delta | - \frac{1}{2} c) & ( \mbox{otherwise} ) \end{cases}\]また $f$ が確率的な関数で,その値が0と1の間であり,$f$の定義域全体での積分が1になるケースにおいては,以下の交差エントロピーも頻繁に用いられます.
交差エントロピー
\[e(x_k) = -y_k \log f(x_k)\]上記の関数は絶対誤差を除き,微分可能であるため,仮に想定している関数 $f$ がパラメータ $a$ に関して微分可能であれば,誤差の合計 $E$ もまたパラメータの微分 $a$ の偏微分として,
\[\frac{\partial E}{\partial a} = \sum_{k=1}^{n} \frac{\partial e}{\partial \delta} \frac{\partial \delta}{\partial f} \frac{\partial f}{\partial a}\]のようにして求めることができます.一般に数値計算によって関数の最小値を与える計算は微分の情報を使うため,この性質はとても重要になります (詳しく知りたい人は「最急降下法」や「ニュートン法」について調べると良いでしょう).
最小二乗法による多項式近似
上記の誤差関数のうち,二乗誤差を最小化するようにパラメータを決定する方法を 最小二乗法 (least squares method) と言います (まれに「最小自乗法」とする文献もある).
ここでは,最小二乗法を用いて多項式の $f$,すなわち
\[f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_m x^{m}\]のパラメータ $a_0, a_1, \ldots, a_m$ を求めてみます.まずは,既知のデータ $(x_k, y_k)$が$n$個 ($k=0, 1, \ldots, n -1$)に対して二乗誤差関数の定義に従い,$E$を書き下してみます.
\[E = \sum_{k=0}^{n-1} ( a_0 + a_1 x_k + \cdots + a_m x_k^{m} - y_k )^2\]このとき,すると$a_i$ ($i = 0, 1, \ldots, m$)を求めるには,各$a_i$による $E$ の微分が 0 となる場所を探せば良いはずなので,次のような等式が満たされれば良いことになります.
\[\frac{\partial E}{\partial a_i} = 2 \sum_{k=0}^{n-1} x_k^{i} \left( a_0 + a_1 x_k + \cdots + a_{m} x_k^{m} - y_k \right) = 0\]この等式が係数 $a_0, a_1, \ldots, a_{m}$ の分だけあるので,実際にはこれらの係数の値は連立方程式の解として与えられることが分かります.この連立方程式が行列の形式で,
\[\mathbf{K p} = \mathbf{q}\]と書けるとするなら, $\mathbf{K} \in \mathbb{R}^{(m+1) \times (m+1)}, \mathbf{p} \in \mathbb{R}^{m+1}, \mathbf{q} \in \mathbb{R}^{m+1}$ はそれぞれ以下のように書ける (添字の番号が0から始まるように書いている)
\[\begin{aligned} K_{ij} &= 2 \sum_{k=0}^{n-1} x_k^{i + j} \\ p_i &= a_i \\ q_i &= 2 \sum_{k=0}^{n-1} x_k^{i} y_k \end{aligned}\]のように与えられます.従って,この連立方程式を解くことで,多項式の係数 $a_0, a_1, \ldots, a_m$ が求まります.
課題2 (配点: 4点)
最小2乗法により近似多項式を求める関数を作成せよ.
関数のプロトタイプ宣言は,
int least_square(matrix *a, matrix points, int order);
とし,行列 points で与えられた点列に対する,order 次の近似多項式の各係数を,列ベクトル *a に書き込むものとする.この時,上記の行列のサイズが (order+1) x (order+1) となることに注意すること.関数の返値は,計算成功=0,計算失敗=1とする.
また第2引数の points 長さが $n$ のデータ列に対して $n \times 2$ の大きさを持つ行列であるとし,1列目に $x_1, x_2, \ldots, x_n$,2列目に $y_1, y_2, \ldots, y_n$ が格納されているものとする.
課題の作成手順
まず,この課題用のZIPファイルをダウンロード後,展開してできるディレクトリを授業用ディレクトリに配置します.例えば,授業用ディレクトリがprogの場合,展開してできるディレクトリ(名前は least_square) は ~/prog/least_square に配置してください.このディレクトリに含まれるMakefile はこの作業ディレクトリ内に ~/prog/include と ~/prog/lib のようにヘッダファイルとライブラリを格納するフォルダが用意されていて, matrix ライブラリが正しく設置されていることを前提にしています.異なるディレクトリ構造の場合には適宜 Makefile を書き換えてください.
ダウンロードしたディレクトリに least_square.c を作成し,以下のテンプレートに従って least_square 関数を完成させてください.
#include <math.h>
#include "matrix.h"
int least_square(matrix *a, matrix points, int order) {
// この中身を実装してください.
return 0;
}
関数を作成後,ディレクトリにある Makefile を用いて make を実行すると check_least_square.c と合わせてプログラムが作成されます.なお,作成されるプログラムの名前は least_square となるので,シェルから ./least_square とタイプして実行すること.
作成された least_square のプログラムは,OpenGL というライブラリ(詳細は後ほど授業で扱います)を利用しており,ウィンドウにグラフが表示されます.Cygwin で OpenGL を使ったプログラムを実行するには,以下のコマンドで X Window (Unix や Linux で使われているウィンドウシステム)を起動しておく必要があります.
システムの実行にはCygwinから
startxwin
とタイプして X Windowを立ち上げます.すると,次に,(下図を参照しつつ)画面右下の通知領域トレイに”X”のアイコンで右クリック,Applications 中の xterm を選択してください.
正しくX Windowからxtermが実行できると,背景が白いターミナルが出てくるので,そのターミナル上でプログラムを実行します.
./least_square
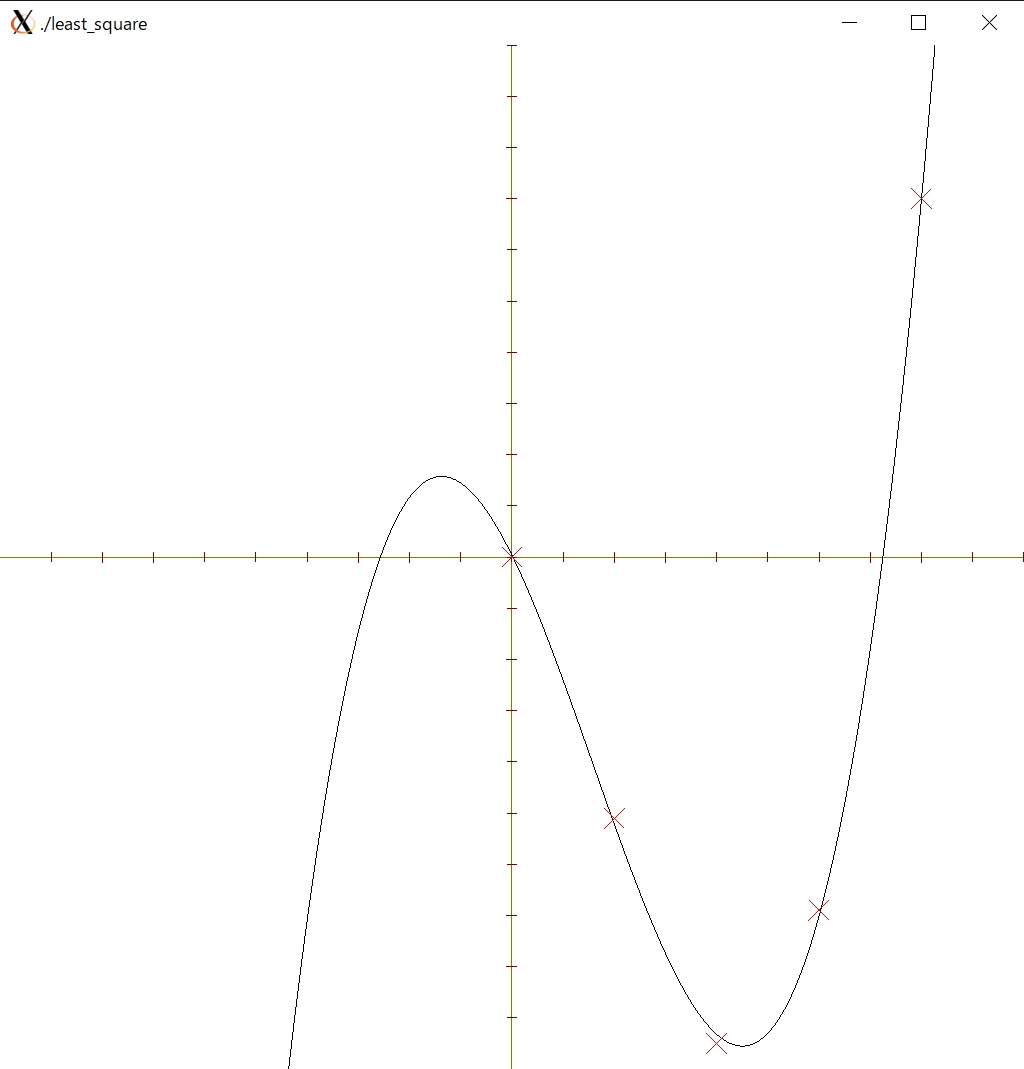
実行に成功すると,ターミナル上に
a_0 = 0.03176
a_1 = -2.036772
a_2 = -0.514980
a_3 = 0.109838
と表示され,以下のようなウィンドウが表示されます.なお,この画面ではマウスの左ドラッグでグラフの移動,右ドラッグで拡大・縮小ができます.またウィンドウはESCかQを押すと閉じます.
補間
補間は,一般には与えられた離散データがどのような関数であるかが不透明である場合に用います.そのため,近似で行ったような,決まり切った関数の未知パラメータを決定するものとは異なる問題を解いていきます.
補間には補間関数と呼ばれる,一定の区間をなめからな関数で表現するために関数が用いられます.この補間関数には様々なものが存在しますが,特に多項式の補間関数を補間多項式と呼びます.
補間によって,与えられる補間多項式が一つに決まるケースは,$n$次多項式を求めるために,$n+1$個の離散データが与えられている場合です.例えば,一次関数であれば,2点があれば直線が一つに決まり,二次関数であれば3点あれば放物線が一つに決まります.
今,ある補間多項式を
\[y = f(x) = a_1 + a_2 x + a_3 x^2 + \cdots a_{n+1} x^n\]と表したとします.これに対して,$(x_1, y_1), \ldots, (x_{n}, y_{n}), (x_{n+1}, y_{n+1})$ という離散データが与えられたならば,各$(x_k, y_k)$に対して,
\[a_1 + a_2 x_k + a_3 x_k^2 + \cdots + a_{n+1} x_k^n = y_k\]という等式が得られるので,これを全ての $(x_k, y_k)$ に対して考え,それらから与えれる連立方程式を行列表示で書き直せば,以下のような式が得られます.
\[\begin{pmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^n \\ 1 & x_2 & x_2^2 & \cdots & x_2^n \\ 1 & x_3 & x_3^2 & \cdots & x_3^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n+1} & x_{n+1}^2 & \cdots & x_{n+1}^n \\ \end{pmatrix} \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n+1} \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n+1} \end{pmatrix}\]この式に置いて係数部分に現れる$x$のべき乗を成分に持つ行列を ファン・デル・モンド行列 と呼びますが,この行列は$x_1, x_2, \ldots, x_{n+1}$に同じものがなければ,正則行列 (逆行列を持つ行列のこと) となることが知られています.そのため,上記の行列方程式をガウスの消去法などでとけば,補間多項式の係数を定めることができそうです.
ところが,上記の行列は $x$ と $x^n$ の両方が行列の成分に入っており,これらの値の間には大きな大小差があることが見込まれます.このような大小差のある行列を数値的に解くと,計算過程において大きな誤差が生じることが知られています.この数値計算において生じる誤算の大きさを見積もる指標に 条件数 と呼ばれるものがあり,最も一般的と思われる定義では,絶対値が最大の固有値と絶対値が最小の固有値の比が条件数になります.
直感的に分かりやすい別の定義を用いれば,条件数は絶対値が最大の行列要素と絶対値が最小の行列要素の比になりますので,ファン・デル・モンド行列の条件数が相当に大きくなることは予想がつきます (条件数の定義の差について説明するには「ノルム」の概念が必要になりますので,ここでは省略します).
いずれにしても,上記の行列方程式を数値的に解くのでは,あまり良い解が得られないことが多く,そのため,これを数学的に解くことで得られる解を用いて,補間多項式の係数を表現します.この結果として得られる補間多項式をラグランジュの補間多項式と呼びます.
ラグランジュの補間多項式
$n$ 個の離散データ $(x_1, y_1), \ldots, (x_{n}, y_{n})$ により与えられるラグランジュの補間多項式は以下のようなものです.
まず,関数 $L_i(x)$を以下のように定義します.
\[\begin{aligned} L_i(x) &= \prod_{j=1, j \neq i}^{n} \frac{x - x_j}{x_i - x_j} \\ &= \frac{(x - x_1) \cdots (x - x_{i-1}) (x - x_{i+1}) \cdots (x - x_{n})}{(x_i - x_1) \cdots (x_i - x_{i-1}) (x_i - x_{i+1}) \cdots (x_i - x_{n})} \end{aligned}\]この式をラグランジュの補間多項式と呼び,これにより得られる
\[p(x) = \sum_{i=1}^{n} L_i(x) y_i\]が補間結果として得られる曲線の式になります.実際,ラグランジュの補間多項式に$x_k$を代入すると,
\[L_i(x_k) = \begin{cases} 0 & (i \neq k) \\ 1 & (i = k) \end{cases}\]が満たされるので,確かに,各離散データに含まれる点を通ることが分かります.
課題3 (配点: 4点)
ラグランジュの補間多項式に基づき,補間を与える関数を作成せよ.
関数のプロトタイプ宣言は,
double lagrange(double x, matrix points);
とし,行列 points で与えられた点列に対する補間多項式を求め,$x$ における補間値を関数の返値として返すこととする (この関数は,補間値を返すものであり,least_squareのように,多項式の係数を返すものではないことに注意)
また第2引数の points 長さが $n$ のデータ列に対して $n \times 2$ の大きさを持つ行列であるとし,1列目に $x_1, x_2, \ldots, x_n$,2列目に $y_1, y_2, \ldots, y_n$ が格納されているものとする.
課題の作成手順
まず,この課題用のZIPファイルをダウンロード後,展開してできるディレクトリを授業用ディレクトリに配置します.例えば,授業用ディレクトリがprogの場合,展開してできるディレクトリ(名前は lagrange) は ~/prog/lagrange に配置してください.このディレクトリに含まれるMakefile はこの作業ディレクトリ内に ~/prog/include と ~/prog/lib のようにヘッダファイルとライブラリを格納するフォルダが用意されていて, matrix ライブラリが正しく設置されていることを前提にしています.異なるディレクトリ構造の場合には適宜 Makefile を書き換えてください.
ダウンロードしたディレクトリに lagrange.c を作成し,以下のテンプレートに従って lagrange 関数を完成させてください.
#include <math.h>
#include "matrix.h"
double lagrange(double x, matrix points) {
// この中身を実装してください.
return x;
}
関数を作成後,ディレクトリにある Makefile を用いて make を実行すると check_lagrange.c と合わせてプログラムが作成されます.なお,作成されるプログラムの名前は lagrange となるので,シェルから ./lagrange とタイプして実行すること.
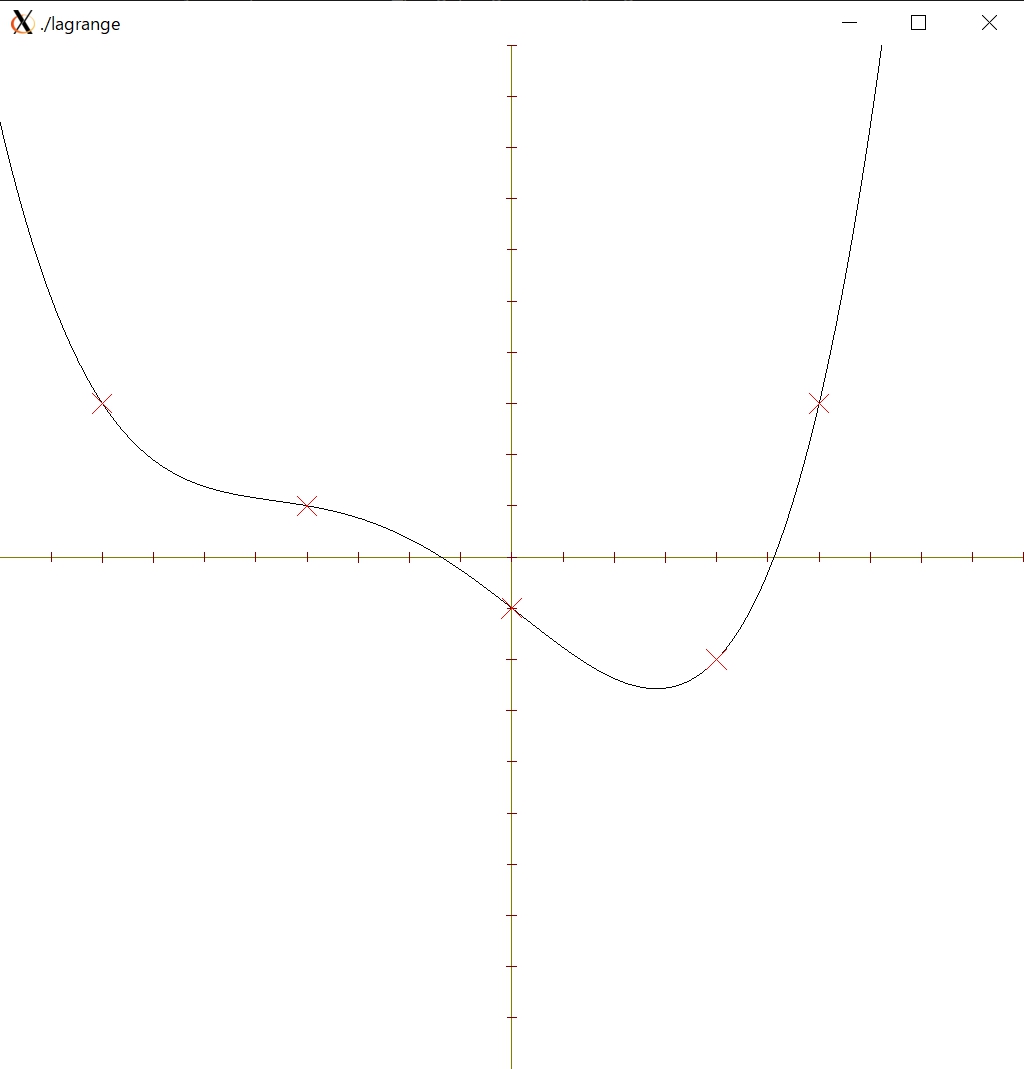
実行に当たっては近似の課題と同様にX Windowからxtermから行う.実行に成功すると,以下のようなウィンドウが表示されます.なお,この画面ではマウスの左ドラッグでグラフの移動,右ドラッグで拡大・縮小ができます.またウィンドウはESCかQを押すと閉じます.
補遺: ラグランジュ補間の問題点
ラグランジュ補間により $n+1$ 個の点を補間すると,補間多項式は,$n$ 次であるため $n-1$ 個の極値を有します.そのため,例えば,
{ -4.0, -3.0 },
{ -2.0, -2.7 },
{ 0.0, 0.0 },
{ 2.0, 6.0 },
{ 4.0, 1.0 },
{ 6.0, -3.0 }
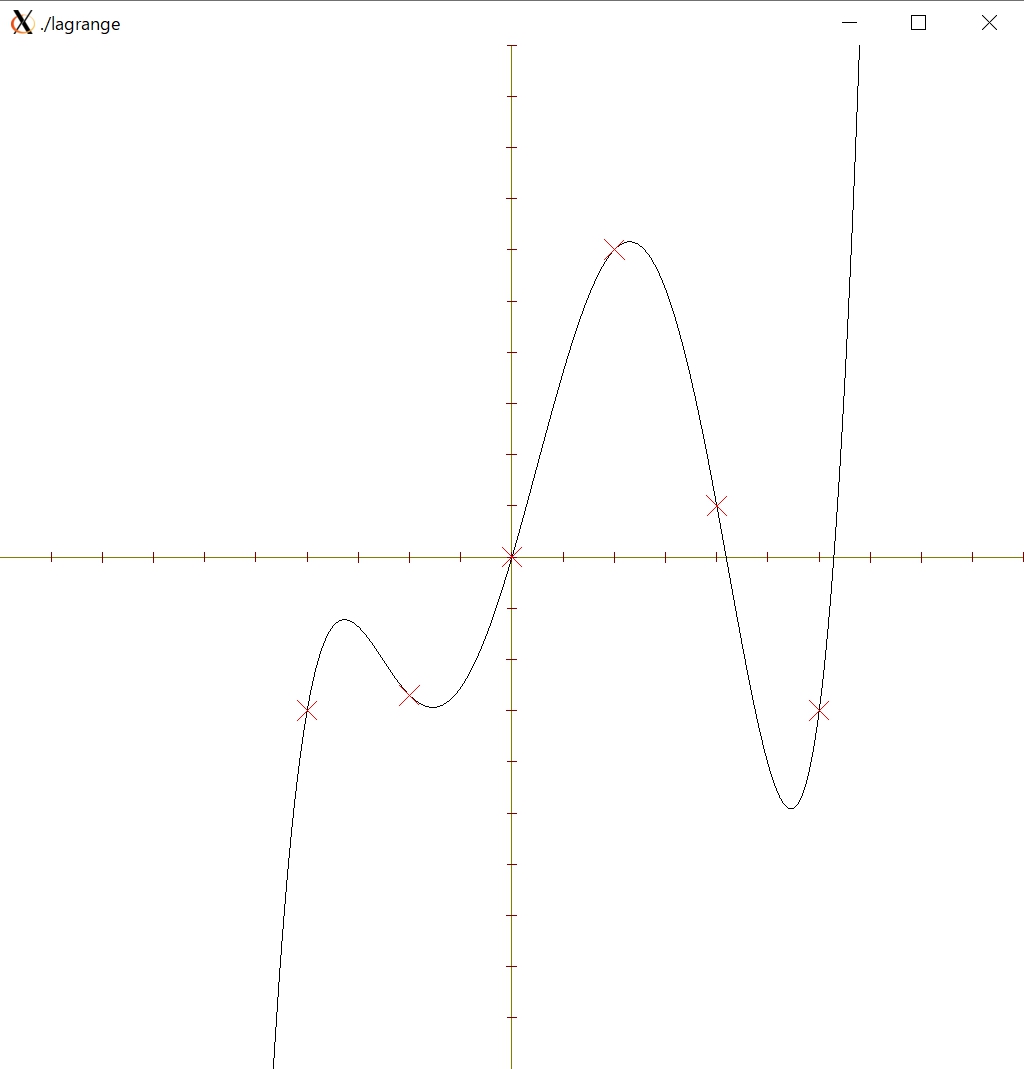
のような6個の点を与えてみると,補間結果は,
のようになり,その曲線は大きく波打ちます(4個の極値が存在するため).特に,両端の点の付近において,波打ちが顕著となります.そのため,多数の点列を滑らかにつなぎたい場合には,Lagrange補間は適切な補間方法とはいえません.
多数の点列を滑らかに補間する曲線を得たい場合には,スプライン補間が用いられます.スプライン補間では,全体を細かい部分(セグメント)に分割し,セグメント間の接続条件を考慮しながら,各セグメントごとに補間式を計算します.スプライン補間については,この授業では触れないので,興味のある人は,各自調べてみてください(特にコンピュータグラフィクスに興味のある人にとっては,スプライン補間はとても重要です).